Paul Park: Baby Names
Data
Data of baby names can be downloaded from the Social Security Administration.
- 5.5M entries
- 30K unique names
- years range from 1910 to 2014
- names have been restricted to those with at least 5 occurrences per year per state
- data must be read in separately for each state
- each row contains state, gender, year, name, and count
- the data seems well formatted, which is perhaps the benefit of using an established government site as a resource
- because data is read in as a string, numbers must be converted
Questions
- What is the most popular name of all time?
- Measuring gender ambiguity of a name
- Baby birth in the US
- Measuring popularity change of a name
What is the most popular name of all time?
It is quite interesting that the top 5 are dominated by male names. One might hazard a guess that there are more to choose from or come up with for female names, and it turns out there are about 13K unique names for males and 20K unique names for females. Given that there were about 30K unique names recorded, about 3000 names are given to both male and female babies, which we will address next.
| rank | name | count |
|---|---|---|
| 1 | James | 4957166 |
| 2 | John | 4845414 |
| 3 | Robert | 4725713 |
| 4 | Michael | 4312975 |
| 5 | William | 3839236 |
Just for female names, here are the top 5:
| rank | name | count |
|---|---|---|
| 1 | Mary | 3730856 |
| 2 | Patricia | 1567779 |
| 3 | Elizabeth | 1500462 |
| 4 | Jennifer | 1461813 |
| 5 | Linda | 1446300 |
Mary is an overwhelming first and also happened to be sixth for all names.
Measuring gender ambiguity of a name
There are two factors that should be considered when measuring gender ambiguity
- absolute difference in gender count for a given name
- total count of a given name
The absolute difference between gender counts can be used as a signal, where the smaller the number, the more gender ambiguous we would think of the name.
The total count of the names should matter too, since it gives us a way to weight results if the gender count difference for two names happen to be the same. Consider for instance, name1 and name2, where the gender count (male, female) is (4, 2) and (100, 102) respectively. It would be reasonable to say that name2 is more gender ambiguous than name1 despite the fact that the difference in gender count is 2 for both. We can incorporate this approach by dividing the absolute difference by the average name count of male and females for each name.
The last safety measure I would like to add accounts for the case when the absolute difference turns out to be zero. Again, consider a case where name1 and name2 have gender counts (4, 4) and (100, 100) respectively. Again, I would consider name2 to be more gender ambiguous because it has more use cases, but dividing the absolute difference by average name count will yield zero for both: 0/4 and 0/100. To resolve this, I will add something like a smoothing factor (= 5) to both the numerator and the denominator such that we can distinguish between the two names so the measure will be (0+5)/(4+5) = 5/9 and (0+5)/(100+5) = 5/105. The ambiguity measure will now perform as we would expect it.
Note that the measure will range from 0 to 1, where the closer the measure is to 0, the more gender ambiguous we would consider the name. The case where the measure equals 1 is when the name is only given to males or females e.g. gender counts of (m, 0) or (0, f) will lead to measures of (m+5)/(m+5) or (f+5)/(f+5), which equal one.
While it would have been nice to aggregate the names for all time, this proved too much for my computer to handle. For year 2014, here are what the rankings look like:
| rank | name | M_count | F_count | abs_diff | avg | measure |
|---|---|---|---|---|---|---|
| 1 | Landry | 224 | 222 | 2 | 223.0 | 0.0307 |
| 2 | Azariah | 208 | 222 | 14 | 215.0 | 0.0864 |
| 3 | Jael | 89 | 94 | 5 | 91.5 | 0.1036 |
| 4 | Jaidyn | 78 | 74 | 4 | 76.0 | 0.1111 |
| 5 | Oakley | 363 | 321 | 42 | 342.0 | 0.1354 |
| 6 | Aven | 49 | 52 | 3 | 50.5 | 0.1441 |
| 7 | Charlie | 1655 | 1421 | 234 | 1538.0 | 0.1549 |
| 8 | Reilly | 52 | 48 | 4 | 50.0 | 0.1636 |
| 9 | Skyler | 893 | 1050 | 157 | 971.5 | 0.1659 |
| 10 | Lennon | 302 | 358 | 56 | 330.0 | 0.1821 |
Andrew Follows from FiveThirtyEight wrote an article about this, and I believe he incorporates data starting from 1910 to 2013, but does not go into trying to rank gender ambiguity.
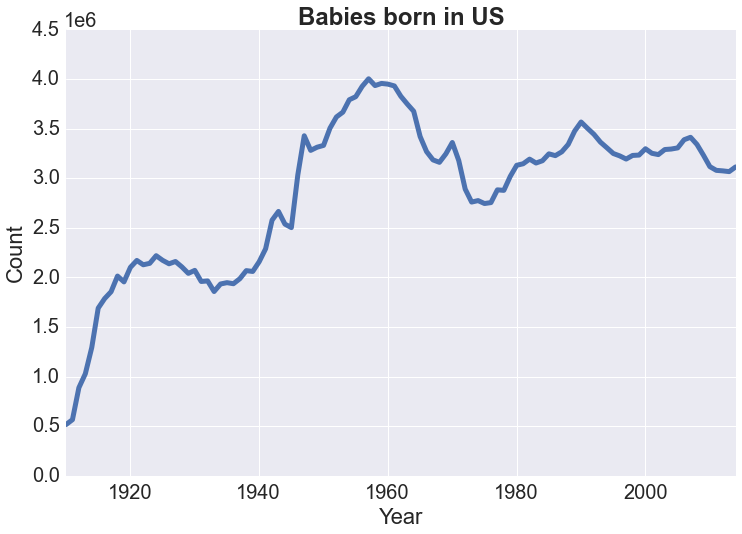
Baby birth in the US
Assuming excluded names are negligible, look at number of babies born in the US over the years. The baby boomer years show up quite prominently. We could also consider number of births by gender, and it is perhaps alarming to see that the number of female babies born has lagged behind that of male babies consistently on the order of thousands since the 1950s...
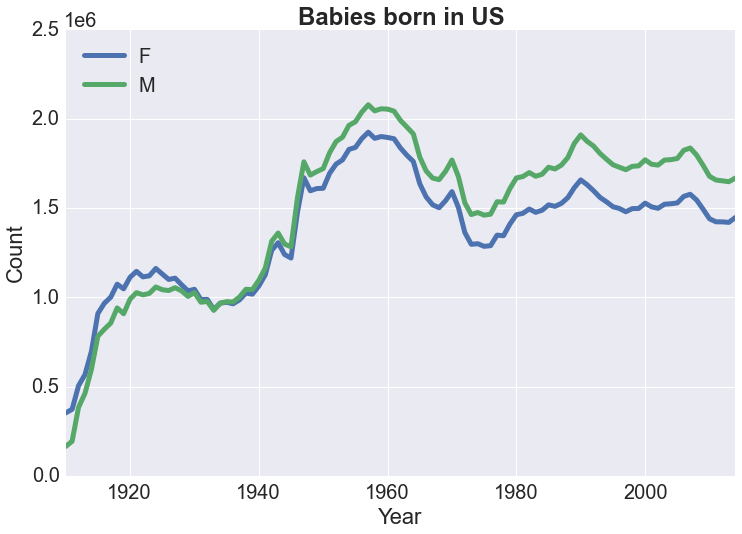
Perhaps we could also estimate for the total population as well. Below is the cumulative sum of the number of births in the US based on recorded names. Assuming a life expectancy of 75 years, the estimate of the total population for a given year should be the cumulative sum of 75 years up to that point, which is also shown below:
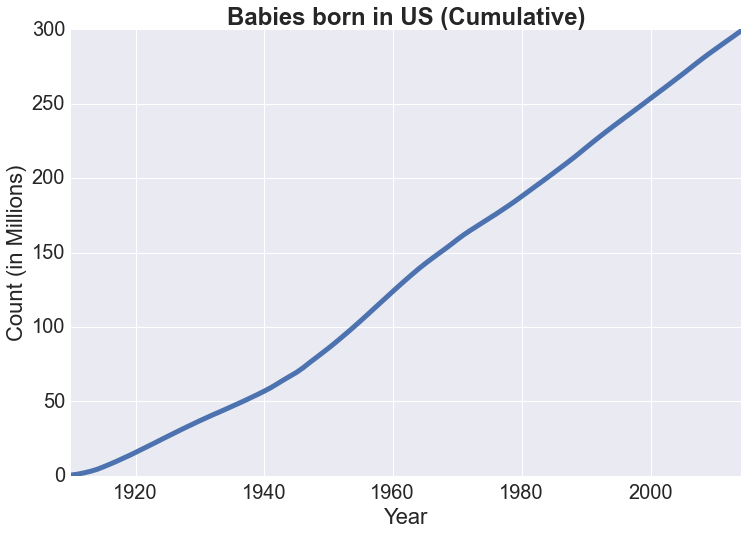
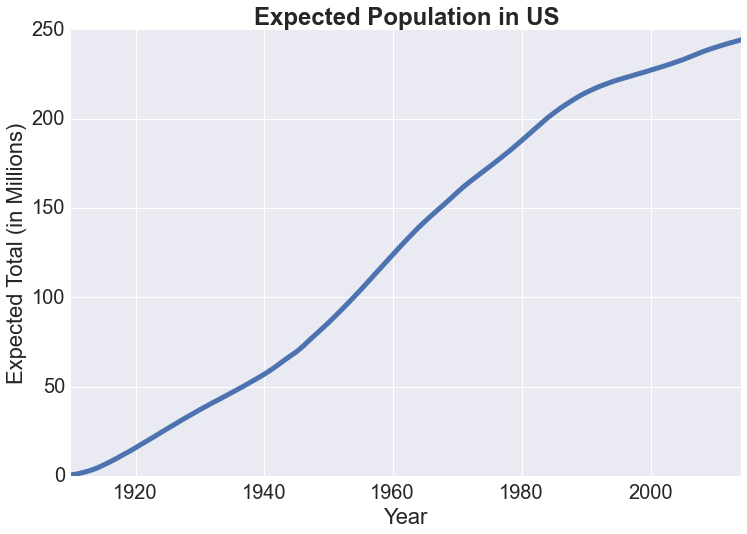
Unfortunately, we only have data starting from 1910, so it is only starting from 1984 that we would have some reliable estimate of the total population:
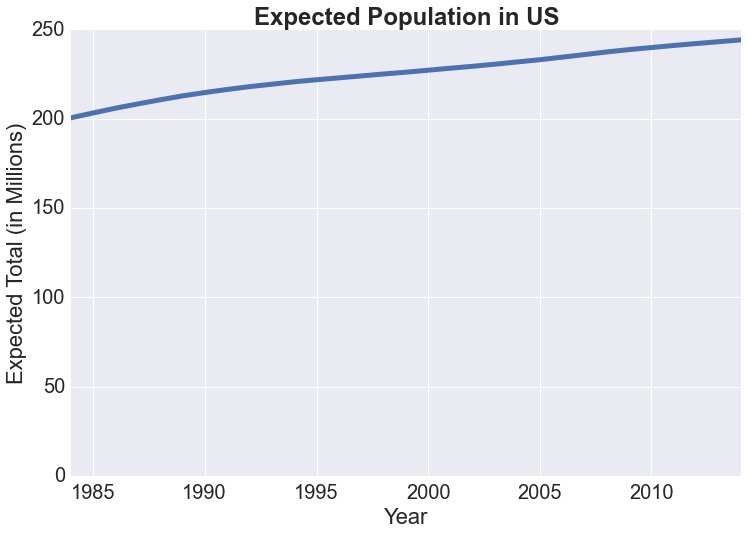
Our estimate ranges from 200M to 250M with an increasing trend and is off by about 50M on average every year. Considering the fact that the data does not include all names, that the average life expectancy is not 75 for all years, and that we are not accounting for immigration, whose number seems to be a quarter of that of baby births in recent years (every 8 seconds a baby is born vs every 33 seconds 1 immigrant (net) is accepted into the US at the time of this writing), our estimate seems pretty reasonable.
Measuring popularity change of a name
Popularity is an interesting concept that I had not really given much thought about until now. It comes up in many different contexts, but within the scope of baby names, it is one thing to answer what is the most popular name of all time, and somewhat another to answer what is the change in popularity of a name over time. One could easily say measure the fraction of the number of babies with a given name for all years and plot it, but given that there are 30K unique names, how should we visualize that, and perhaps a more important question is whether such a plot matters in the first place.
As far as utility is concerned, for me personally, I am purely interested in knowing (who doesn't care about popularity?), and it seems to me that change in popularity is something that we should be able to measure in some tangible way. That said, visualization is still an issue, so for now, we need a method for choosing names of interest just to see if anything significant is occurring. So what I would like to do is just measure the change in popularity for the top 10 baby names for males and females separately. But before we get to that point, I need to prep the data to determine the fraction that a given name occupies.
Next Steps?
Guessing the state in which a person was born based on name
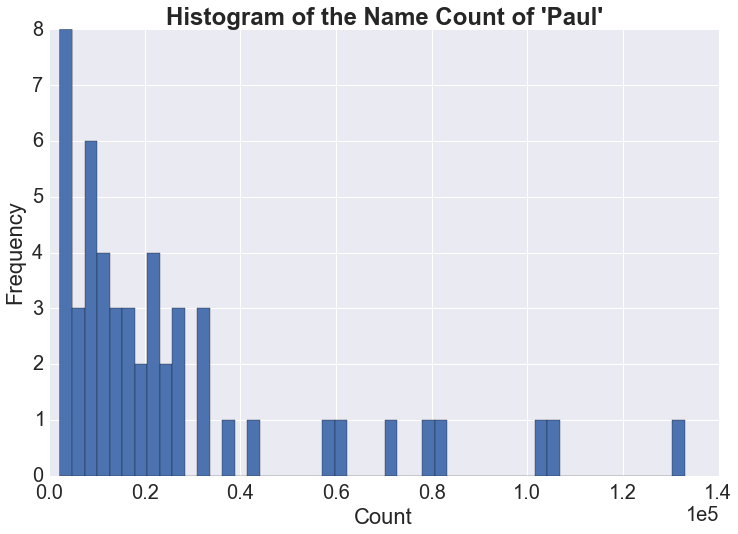
Nate Silver and Allison McCann at FiveThirtyEight have done some interesting analysis on trying to guess a person's age based on name by using external data such as actuarial life tables with estimates of death rates. Perhaps another question one could ask with the available data is where a person was born based on name. Just to start off, I wanted to know which state had the most number of babies named Paul for all time, as well as the distribution of the counts. Using the analysis from FiveThirtyEight as additional information for a person's age might be helpful as well.
| rank | state | count |
|---|---|---|
| 1 | NY | 132950 |
| 2 | PA | 104582 |
| 3 | CA | 102820 |
| 4 | OH | 81215 |
| 5 | MA | 78268 |