PRELIMINARIES
* Illustration: Mixing of viscoelastic fluids
Mixing: From Large to Small Scales
* Illustration: Typical mixing in polymer processing
* Illustration: Role of dispersed phases on flow structure
Affine Deformation
* Illustration: Stretching of low-viscosity-ratio elongated drops
* Illustration: Satellite formation in capillary breakup
* Illustration: Comparison between necking and capillary breakup
* Illustration: Drop size distributions produced by chaotic flows
* Illustration: Effect of viscosity ratio on drop size distributions
HEURISTICS
Small Scales: Particle Interactions
Erosion
* Illustration: Simultaneous erosion and rupture
Erosion Controlled Fragmentation
* Illustration: Aggregation of area-conserving clusters in chaotic flows
* Illustration: Aggregation of fractal structures in chaotic flows
REFERENCES
FIGURE CAPTIONS
Note on Notation
Relations from breakup, coalescence, fragmentation and aggregation are based on either actual experiments or numerical simulations, the latter commonly referred to as "computer experiments." Computer experiments are often based on crude simplifying assumptions and actual experiments are always subject to errors; the strict use of the equality sign in many of the final results may therefore be misleading. In order to accurately represent the uncertainty associated with the results, the following notation is adopted:
~ Used to denote proportionality.
Used in conditional statements when the limiting value given is correct within a factor of 2.
=, >, < Used in expressions related to modeling and standard mathematical manipulations.
Mixing and dispersion of viscous fluids -- blending in the polymer processing literature -- is the result of complex interaction between flow and events occurring at drop length-scales: breakup, coalescence and hydrodynamic interactions. Similarly, mixing and dispersion of powdered solids in viscous liquids is the result of complex interaction between flow and events -- erosion, fragmentation and aggregation -- occurring at agglomerate length scales. Important applications of these processes include the compounding of molten polymers, and the dispersion of fine particles in polymer melts. Reynolds numbers in both cases are small, even more so given the small length scales that dominate the processes.
There are similarities and, undoubtedly, substantial differences between these two processes. The following analogies are apparent (Figure 1):
coalescence - aggregation
These similarities notwithstanding, it may be argued however, that it is differences that have hindered understanding. This state of affairs has not been helped by proliferation of terminology: alloying, compounding, and blending all appear in the polymer processing literature; fragmentation and rupture in the solids dispersion literature; breakup, rupture, and burst in the fluid mechanics literature. Both agglomerates and flocs refer to particle clusters. Undoubtedly droplets are easier to deal with than agglomerates whose structure is complex and can only be known in a statistical sense. Thus breakup and coalescence, being placed squarely in the realm of classical fluid mechanics, are on more sure footing than fragmentation and aggregation, which demand knowledge of physical chemistry and colloid science, and have been studied to a lesser extent.
Realistic mixing problems are inherently difficult owing to the complexity of the flow fields, the fact that the fluids themselves are rheologically complex, and to the coupling of length scales. For this very reason, mixing problems have been attacked traditionally on a case-by-case basis. Modeling becomes intractable if one wants to incorporate all details at once. Nevertheless it appears important to focus on common features and to take a broad view.
Two reviews, published in the same book, may be considered to be the launching basis for the material presented here: Meijer and Janssen (1994) and Manas-Zloczower (1994). In both reviews the fundamentals of the processes are considered at a small length scale (drops, agglomerates), focusing on the effects of flow. Meijer and Janssen (1994) review fundamental studies of droplet breakup and coalescence in the context of the analysis of polymer blending. Manas-Zloczower (1994), on the other hand, focuses on dispersion of fine particles in polymers. The primary objective of the present work is to present both topics in a unified format together with the basics of particle aggregation. The unified presentation serves to highlight the analogies between the processes and consequently to increase understanding. A related goal is to introduce potentially useful recent advances in fundamentals which have not yet been applied to the analysis of practical processing and structuring problems (Villadsen 1997).
There have recently been substantial advances in the understanding of viscous mixing of single fluids. This has been driven primarily by theoretical developments based on chaos theory and increased computational resources as well as by advances in fluid mechanics and a host of new experimental results. Such an understanding forms a fabric for the evolution of breakup, coalescence, fragmentation and aggregation. These processes can in fact be viewed as a population of "microstructures" whose behavior is driven by a chaotic flow; microstructures break, diffuse, and aggregate, causing the population to evolve in space and time. Self-similarity is common to all these problems; examples arise in the context of the distribution of stretchings within chaotic flows, in the asymptotic evolution of fragmentation processes, and in the equilibrium distribution of drop sizes generated upon mixing of immiscible fluids.
It may be useful at this juncture to draw the distinction between theory and computations (or numerical experiments) as the material presented here is somewhat tilted towards theory. Computations are not theory, but theory often requires computations. To the extent that it is not possible to put all elements of a problem into a complete picture, assumptions are necessary -- often entailing mechanistic views of the behavior of the system. Non-trivial assumptions leading to non-trivial consequences lead to significant theories. Assuming that a flow field can be imagined as an assembly of weak regions (where stretching of passive elements is linear) and strong regions (where stretching of passive elements is exponential) could form the basis of a theory; real flows are manifestly more complex but this is clearly a useful approximation. In fact, G. I. Taylor's (1932) pioneering work in drop dynamics can be traced back to this crucial element. A binary breakup assumption, on the other hand, may not form as strong a basis, especially if more precise knowledge can be incorporated with little or no difficulty into the picture: Drops and fluid filaments break, producing often in single events, a distribution of sizes. Thus a "theory" based on binary breakup could be revisited, and may be successfully augmented. Similar comments apply to fragmentation of agglomerates.
This paper is divided into two main, interconnected parts -- breakup and coalescence of immiscible fluids, and aggregation and fragmentation of solids in viscous liquids -- preceded by a brief introduction to mixing, this being focused primarily on stretching and self-similarity.
The treatment of mixing of immiscible fluids starts with a description of breakup and coalescence in homogeneous flows. Classical concepts are briefly reviewed and special attention is given to recent advances -- satellite formation and self-similarity. A general model, capable of handling breakup and coalescence, while taking into account stretching distributions and satellite formation is described.
The treatment of aggregation and fragmentation processes parallels that of breakup and coalescence. Classical concepts are briefly reviewed; special attention is given to fragmentation theory as well as to flow-driven processes in nonhomogeneous (chaotic) flows. The Péclet number in all instances is taken to be much greater than unity, so that diffusion effects are unimportant. In many examples, hydrodynamic interactions between clusters are neglected to highlight the effects of advection on the evolution of the cluster size distribution and the formation of fractal structures.
The paper is structured to be read at three levels. The main thread of the text is a review of fundamentals and previous studies. Illustrations focusing on specific systems or more detailed elaboration of concepts are interspersed in the text. Many of these include new results; they form a second level which can be read as independent subunits. Finally, the conclusions of each section especially those, with significance for practical applications, are summarized as heuristics.
STRETCHING AND CHAOTIC MIXING
Fluid advection -- be it regular or
chaotic -- forms a template for the evolution of breakup, coalescence,
fragmentation and aggregation processes. Let v(x,t) represent the
Eulerian velocity field (typically we assume that ![]() ). The solution of
). The solution of
with X representing the initial coordinates of material particles located at x at time t, gives the motion
i.e., the particle X is mapped to the position x after a time t. This is formally the solution to the so-called advection problem (Aref, 1984). The foundations of this area are now on sure footing and reviews are presented in Ottino (1989, 1990). The quantity of interest is stretching of fluid elements.
The stretches of a material filament dx, l, and material surface element da, h, are defined as
![]() ,
, ![]() (3)
(3)
where dX and dA represent the initial conditions of dx and da respectively. The fundamental equations for the rate of stretch are
where Dº[Ñv+(Ñv)T] /2 is the stretching tensor, and m and n are the instantaneous orientations (m=dx/|dx|, n=da/|da|). The Lagrangian histories d(lnl)/dt=al(X,M,t) and d(lnh)/dt =ah(X,N,t), are called stretching functions. Flows can be compared in terms of their stretching efficiencies. The stretching efficiency, el=el(X,M,t) of the material element dX and the stretching efficiency eh=eh(X,N,t) of the area element dA are defined as
If ![]() , ei
<(1/2)1/2 in two-dimensional (2D) flows and
(2/3)1/2 in three-dimensional (3D) flows, where
i=l,h. The
efficiency can be thought of as the specific rate of stretching of material
elements normalized by a factor proportional to the square root of the energy
dissipated locally.
, ei
<(1/2)1/2 in two-dimensional (2D) flows and
(2/3)1/2 in three-dimensional (3D) flows, where
i=l,h. The
efficiency can be thought of as the specific rate of stretching of material
elements normalized by a factor proportional to the square root of the energy
dissipated locally.
The key to effective mixing lies in producing stretching and folding, an operation that is referred to in the mathematics literature as a horseshoe map. Horseshoe maps, in turn, imply chaos. The 2D case is the simplest. The equations of motion for a two-dimensional area preserving flow can be written as
where y is the stream function. If the velocity field is steady, (i.e., y is independent of time) then it is integrable and the system cannot be chaotic. The mixing is thus poor: stretching for long times is linear; the stretching function decays as 1/t, and the efficiency decays to zero. On the other hand, if the velocity field, or equivalently y, is time-periodic there is a good chance that the system will be chaotic (Aref, 1984). It is relatively straightforward to produce flow fields that can generate chaos; a necessary condition for chaos is the "crossing" of streamlines; two successive streamline portraits, say at t and (t+DT) for time periodic flows or at z and (z+Dz) for spatially periodic flows, when superimposed, should show intersecting streamlines. In 2D systems this can be achieved by time modulation of the flow field, for example by motions of boundaries or time periodic changes in geometry. Figures 2 and 3 show typical examples of mixing in such flows: the vortex mixing flow (VMF) and the cavity flow, respectively. The vortex mixing flow is generated by alternately rotating one of the cylinders for a fixed period of time, while the cavity flow is generated by alternately moving the upper and lower walls of the cavity for a fixed time period. It is clear from the geometry of the systems that both achieve the required "crossing" of streamlines by the time modulation.
Numerous experimental studies have revealed the degree of order and disorder compatible with chaos in fluid flows. Experiments conducted in carefully controlled two-dimensional, time-periodic flows and spatially periodic flows reveal the complexity associated with chaotic motions. The most studied flows are the flow between two rotating eccentric cylinders, several classes of co-rotating and counter-rotating cavity flows, and spatially periodic flows. Even within this theme, many variations are possible. For example, Leong (1990) considered the effect of cylindrical obstructions placed in a cavity flow; Schepens (1996) took this a step further and carried out computations and experiments fo the case when the pin itself is allowed to rotate. The 2D time-periodic case is especially illustrative.
Dye structures of passive tracers placed in time-periodic chaotic flows evolve in an iterative fashion; an entire structure is mapped into a new structure with persistent large-scale features, but finer and finer scale features are revealed at each period of the flow. After a few periods, strategically placed blobs of passive tracer reveal patterns that serve as templates for subsequent stretching and folding. Repeated action by the flow generates a lamellar structure consisting of stretched and folded striations, with thicknesses s(t), characterized by a probability density function, f(s,t), whose mean, on the average, decreases with time (f(s,t)ds is the number of striations with striation thicknesses between s and s+ds). The striated pattern quickly develops into a time-evolving complex morphology of poorly mixed regions of fluid (islands) and of well-mixed or chaotic regions (see Figure 3). Computations capture the evolution of the structure reasonably well for short mixing times (Figures 2 and 3) and are useful for analysis. Islands translate, stretch, and contract periodically and undergo a net rotation, preserving their identity returning to their original locations after multiples of the period of the flow, symmetry being a common feature of many flows (see Figure 4). Stretch in islands, on the average, grows linearly and much slower than in chaotic regions, in which the stretch increases exponentially with time. Moreover, since islands do not exchange matter with the rest of the fluid and they represent an obstacle to efficient mixing. An important parameter of the flows is the sense of rotation in the alternate periods -- corotation tends to produce more uniform mixing.
Duct flows, like steady two-dimensional flows are poor mixers. This class of flows is defined by the following velocity field
which is composed of a two-dimensional cross-sectional flow augmented by a unidirectional axial flow; fluid is mixed in the cross-section while it is simultaneously transported down the duct axis. In a duct flow, the cross-sectional and axial flows are independent of both time and distance along the duct axis, and material lines stretch linearly in time. A single screw extruder, for example, belongs to this class.
Duct flows can be converted into efficient mixing flows (i.e., flows with an exponential stretch of material lines with time) by time-modulation or by spatial changes along the duct axis. One example of the spatially-periodic class, is the partitioned-pipe mixer (PPM). This flow consists of a pipe partitioned with a sequence of orthogonally placed rectangular plates (Figure 5a). The cross-sectional motion is induced through rotation of the pipe with respect to the assembly of plates whereas the axial flow is caused by a pressure gradient; the behavior of the system is characterized by the ratio of cross-sectional twist to axial stretching, b (Khakhar, Franjione and Ottino, 1987a; Kusch and Ottino, 1992). The flow is regular for no cross-sectional twist (b=0), and becomes chaotic with increasing values of b. The KAM (Kolmogorov-Arnold-Moser) surfaces (tubes) bound regions of regular flow, and correspond to the islands in 2D systems (Figure 5b). Experiments reveal the intermingled regular and chaotic regions: A streakline starting in a KAM tube passes through the mixer with little deformation, whereas streaklines in the chaotic regions are mix well (Figure 5c).
The concept of improved mixing by reorienting the flow is often used in various types of single screw extruders. The extruder is divided into a small number of zones with a mixing section between each zone. Each mixing section consists of pins or blades which protrude into the flow and cause random reorientations of fluid elements in the flow; a random reorientation is better than no reorientation at all. The mixing efficiency climbs and mixing is dramatically improved. Such an approach was investigated by Chella and Ottino (1985).
Mixing in such systems can also be significantly improved by means of time-dependent changes in geometry. This idea can be readily implemented in the context of duct flows by adding a secondary baffle. Such a concept has obvious applications in polymer processing; for example, single screw extruders can be imagined as a channel with a moving lid (not shown) as in Figure 6a. A two-dimensional analog of the extruder channel with a baffle is a cavity flow with steady motion of the top wall and periodic motion of the lower wall with a rectangular block (Figure 6b). The mixing in this case is greatly improved as compared to a steady cavity flow. Similar designs have been arrived at empirically in engineering practice.
Illustration: Mixing of viscoelastic fluids
Driving a system faster, for example by moving boundaries at a higher speed under a fixed protocol, does not imply better mixing: islands survive and do not go away. Yet another instance where faster action may actually lead to worse mixing is provided by the case of viscoelastic fluids. Niederkorn and Ottino (1993) studied experimentally and computationally, the mixing of Boger fluids -- viscoelastic fluids with a constant shear viscosity. The system considered was the flow between two eccentric cylinders, in which the inner and outer cylinders are rotated alternately. The flow is referred to as the journal bearing flow and is a classical sytem in chaotic mixing studies. In the limit of slow flow, a Boger fluid behaves as Newtonian; faster flows lead to viscoelastic effects quantified in terms of Weissenberg number (We), the ratio of the relaxation time of the fluid to a time scale of the flow; e.g. the inverse of the shear rate. Spectacular effects occur at moderate We (Niederkorn and Ottino, 1993); Figure 7 shows the contrast between the Newtonian (We»0) and the non-Newtonian case (We»0.06). In general, it appears that viscoelastic fluids mix more slowly than the corresponding Newtonian fluid; in most instances also, in the long time limit, the region occupied by regular islands is larger for the viscoelastic fluid; i.e., the mixing is poorer. This, however, is not always the case and there are experimentally documented instances where the long-time degree of mixing in the viscoelastic case is better than in the Newtonian case. Shear thinning effects, on the other hand, appear to be milder than viscoelastic effects and relatively high degrees of shear thinning are required to produce substantial effects (Niederkorn and Ottino, 1994).
Kumar and Homsy (1996) carried out a theoretical analysis of slightly viscoelastic flow and mixing in the journal bearing system described above. The effect of elasticity on the flow is to shift the stagnation streamline which affects the size of the mixed region (Kaper and Wiggins, 1993). Depending on the mixing protocol, Kumar and Homsy (1996) found that the size of unmixed islands may increase or decrease with elasticity as in the experiments of Niederkorn and Ottino (1994). Many other comparisons between chaotic advection of Newtonian and viscoelastic fluids are possible. For example, the critical modulation frequency of the inner cylinder at which the largest island disappears is lower for the viscoelastic fluid. Conclusions, however, are specific and dependent on mixing protocols, and little can be said in general about the effects of viscoelasticity.
Filaments in chaotic flows experience complex time-varying stretching histories. Computational studies indicate that within chaotic regions, the distribution of stretches, l, becomes self-similar, achieving a scaling limit. The distribution of stretches can be quantified in terms of the probability density function Fn(l)ºdN(l)/dl, where dN(l) is the number of points that have values of stretching between l and (l+dl) at the end of period n. Another possibility is to focus on the distribution of logl. In this case we define the measure Hn(logl)ºdN(logl)/d(logl).
Muzzio, Swanson, and Ottino (1991) demonstrated that the distribution of stretching values in a globally chaotic flow approaches a log-normal distribution at large n: A log-log graph of the computed distribution approaches a parabolic shape (Figure 8a) as required for a log-normal distribution. Furthermore, as n increases, an increasing portion of the curves in the figure (Figure 8b) overlap when the distribution is rescaled as
where mlogl(n) = ?loglHn(logl) is the first moment of Hn(logl) and z=logl/logLg, with logLg = [?loglHn(logl)]/[?Hn(logl)], and the sums are over a large number of fluid elements in the flow. The rescaled distribution is thus independent of the number of periods of the flow (n) at large n, and the distributions Hn(logl) are said to be self-similar.
The explanation for the approach to a log-normal distribution is as follows. Consider, for simplicity, flows as those considered by Muzzio, Swanson and Ottino (1991): two-dimensional time periodic flows. Let ln,k denote the length stretch experienced by a fluid element between periods n and k. The total stretching after m periods of the flow, l0,m, can be written as the product of the stretchings from each individual period:
The amount of stretching between successive periods (i.e., l1,2 and l2,3) is strongly correlated, however the correlation in stretching between non-consecutive periods (e.g., l0,1 and l4,5) grows weaker as the separation between periods increases due to chaos (the presence of islands in the flow complicates the picture, but these issues are not considered here). Thus, l0,m is essentially the product of random numbers, which when rewritten as
gives a sum of random numbers. According to the central limit theorem, any collection of sums of random numbers will converge to a Gaussian. So, when all material elements are considered, the distribution of l0,m should be log-normal (Figure 8a). This conjecture has been verified by numerous computations (Muzzio et al., 1991).
Many practical mixing flows (e.g., single
screw extruder with mixing zones), as well as the chaotic cavity flows discussed
above, are composed of a sequence of shear flows with periodic random
reorientation of material elements relative to the flow streamlines. In all
cases, the effect of the reorientation is an exponential stretching of material
elements. The interval between two successive reorientations is an important
parameter of such systems, and the following argument demonstrates that an
optimum interval must exist at which the total length stretch is maximum for a
fixed time of mixing: In the limit of very small periods, material elements are
stretched and compressed at random, and hence the average length stretch is
small; in the limit of very large time periods, the flow approaches a steady
shear flow and again the length stretch is small. Khakhar and Ottino (1986a)
showed a maximum in the average stretching efficiency when the strain per period
was between 4 and 5 for a simple shear flow and a vortical flow with random
periodic reorientation (Figure 9). Since the average efficiency is simply the
length stretch per period normalized by ![]() , which is proportional to the square
root of the viscous dissipation, the optimum corresponds to the maximum
stretching for a fixed energy input. Similar results are obtained when there is
a distribution of shear rates.
, which is proportional to the square
root of the viscous dissipation, the optimum corresponds to the maximum
stretching for a fixed energy input. Similar results are obtained when there is
a distribution of shear rates.
* In general, time periodic (or spatially periodic) flows generate islands (or tubes). Stretching in islands and tubes is linear. Stretching in chaotic regions is exponential.
* Stretchings of the order of 104 can be obtained in about six cycles (or reorientations). A stretch of about 4-5 per cycle seems to be optimal.
* Corotational flows distribute material better than counterrotational flows.
* Viscoelasticity (We as low as 0.06) results in substantially different patterns of mixing -- larger islands and slower rates of mixing may result.
* Shear thinning, typically, has little effect on mixing.
Physical Picture
The importance of viscous mixing can be justified on purely business grounds. Consider the case of polymers. The world production (by volume) of plastics has surpassed that of metals, and new polymers with extraordinary properties are constantly being produced in laboratories around the world. Less than 2% of all new polymers, however, ever find a route to commercial application. There are two reasons for this low figure. The first is the inherent high cost of producing new materials. The second is that often new properties can be obtained by compounding, blending, and alloying (all synonyms of mixing) existing polymers together with additives, to produce "tailored" materials with the desired properties. Mixing provides the best route to commercial competitiveness while optimizing properties-to-price ratio. Similar arguments can be made the consumer products industry where imparting the "right structure" is crucial to the value of the product (Villadsen 1997).
Quenched, possibly meta-stable structures are ultimately responsible for the properties observed, so the key linkage is between mixing and morphology. Thus for example, the properties of a polymer blend -- e.g., permeability, mechanical properties -- are a strong function of the mixing achieved and this in turn depends strongly on the equipment used. Thin, ribbon-like anisotropic structures are produced in single screw extruders; fine drop dispersions in static mixers and twin screw extruders. Knowledge about the mixing process can be used to produce targeted properties (see for example, Lui and Zumbrunnen 1997).
Experiments reveal mechanisms at work. Figure 10 shows a 45/55 blend of PS/HDPE; the processing temperature is such that the viscosities are nearly matched. Long ribbons of PS in the process of breakup by capillary instabilities, as well as coalesced regions, are apparent in this figure (Meijer et al., 1988). In simple shear flow, the phenomena are somewhat different and pellets may be stretched into sheets which break by the formation and growth of holes (Sundaraj, Dori and Macosko, 1995).
It may appear surprising that large length
reductions -- initial pellet sizes being on the order of a few millimeters,
final drop scales on the order of microns -- can be achieved in short residence
times and relatively low shear rates. For example, in a typical extruder there
are high-shear-zones in which residence times (tres) are short (![]() , tres~0.1 s), and
low-shear-zones with longer residence times (
, tres~0.1 s), and
low-shear-zones with longer residence times (![]() , tres~10 s), with material elements visiting each zone several
times (Janssen and Meijer, 1995). This leads to a strain of about 10 in high
shear zones and 30 in low shear zones which is considerably less than the length
stretches shown in Figure 10. The key to efficient mixing of immiscible liquids,
as in the case of single fluids, lies in reorientations; 6 reorientations, with
a stretch per reorientation of about 5 generates a stretch of 1.5x104.
, tres~10 s), with material elements visiting each zone several
times (Janssen and Meijer, 1995). This leads to a strain of about 10 in high
shear zones and 30 in low shear zones which is considerably less than the length
stretches shown in Figure 10. The key to efficient mixing of immiscible liquids,
as in the case of single fluids, lies in reorientations; 6 reorientations, with
a stretch per reorientation of about 5 generates a stretch of 1.5x104.
A precondition for stretching of initially spherical drops is that hydrodynamic stresses acting on the drop be large enough to overcome surface tension which tends to return the drop to a spherical shape; stretched drops eventually break by surface tension driven instabilities. Complex flow in mixers results also in collisions between dispersed phase drops and, eventually, coalescence if the film between the colliding drops breaks. The dynamic balance between breakup and coalescence, both driven by the flow, determines the distribution of drop sizes and morphology in the blend. Fundamental studies of single drop breakup and coalescence of pairs of drops, mainly for Newtonian fluids, provide a basis for the analysis of the physical processes. The non-Newtonian rheology of blends and the effects of high loading of the dispersed phase (e.g., increase in effective viscosity and phase inversion) complicate the analysis and much remains to be done at a basic level in this regard. Also, little will be said here about the mid-column in Figure 1. The reader interested in this topic will find lead sin the papers by Kao and Mason (1975), for cohesionless aggregates, and Ulbrecht et al. (1982), Stroeve and Varanasi (1984), Srinivasan and Strove (1986), and Varanasi et al. (1994), for the case of double emulsions.
Mixing: From Large to Small Scales
Mixing involves a reduction of length scales. Let us now consider a typical mixing process as it progresses from large to small scales, as illustrated in Figure 11. The initial condition corresponds to a large blob of the dispersed phase (d), suspended in the continuous phase (c). At the beginning of the mixing process, the capillary number, which is the ratio of the viscous forces to the interfacial forces, is large and interfacial tension is unimportant. A description of mixing essentially amounts to a description of the evolution of the interface between the two large masses of fluid: an initially designated material region of fluid (Figure 11, top) stretches and folds throughout space. An exact description of mixing is thus given by the location of the interfaces as a function of space and time. This level of description is, however, rare because the velocity fields usually found in mixing processes are complex, and the deformation of the blobs is related in a complicated way to the velocity field. Moreover, relatively simple velocity fields can produce exponential area growth due to stretching and folding, and numerical tracking becomes impossible. Realistic problems can take years of computer time with megaflop machines (Franjione and Ottino 1987).
The problem of following the interface for Newtonian fluids can be described by the Stokes equations:
where, c denotes the continuous phase and d denotes the dispersed phase. The boundary conditions at the interface come from a jump in the normal stress due to the interfacial tension, s, between the two fluids and the kinematic condition
In addition, the velocity field is continuous across the interface
and boundary conditions at the system
boundaries and the initial condition must be specified. Points in both the
dispersed and continuous phases are denoted by the position vector x and
points at the interface are given by xs. The stress tensors,
Tc and Td, are given
by ![]() ,
where
,
where ![]() . The mean
curvature of the interface is given by
. The mean
curvature of the interface is given by ![]() , where the local normal n is
directed from the dispersed phase to the continuous phase and
, where the local normal n is
directed from the dispersed phase to the continuous phase and ![]() denotes the surface
gradient.
denotes the surface
gradient.
If the length scales associated with changes in velocity are normalized by dv (characteristic length scale for Stokes flow), length scales associated with changes in curvature are normalized by ds (typical striation thickness) and velocities normalized by V (a characteristic velocity), then the normal stress condition becomes,
where p is the viscosity ratio,
md/mc, primed quantities denote
dimensionless variables and, ![]() , may be interpreted as the ratio of
viscous forces, mcV/dv
(V/dv, is the characteristic shear rate) to capillary forces,
s/ds. This ratio is the so-called
capillary number. During the initial stages of mixing Ca is relatively
large due to large striation thicknesses, ds, although interfacial
tension effects may be noticeable in regions of high curvature, such as folds.
However, as the mixing process proceeds, ds is reduced and interfacial
tension starts to play a larger role. The coupling between the flow field and
interfacial tension occurs at length scales of order
, may be interpreted as the ratio of
viscous forces, mcV/dv
(V/dv, is the characteristic shear rate) to capillary forces,
s/ds. This ratio is the so-called
capillary number. During the initial stages of mixing Ca is relatively
large due to large striation thicknesses, ds, although interfacial
tension effects may be noticeable in regions of high curvature, such as folds.
However, as the mixing process proceeds, ds is reduced and interfacial
tension starts to play a larger role. The coupling between the flow field and
interfacial tension occurs at length scales of order ![]() where
where ![]() is a characteristic shear rate
(i.e., Ca=O(1)).
is a characteristic shear rate
(i.e., Ca=O(1)).
Bigg and Middleman (1974) and Chakravarthy and Ottino (1996) approached the problem depicted in Figure 12 by solving the governing equations (A.1)-(A.4) using a modified finite difference technique. Using this method the evolution of the interface can be followed and the length stretch of the interface and striation thicknesses can be obtained. However, this technique eventually breaks down as the interface becomes highly convoluted. Numerical difficulties quickly arise due to the large number of points which must be used to follow the interface. Aletrantive methods for the numerical simulation of the early stages of mixing are presented by Chella and Viñals (1996) and Zumbrunnen et al (e.g. Zhang and Zumbrunnen 1996a,b) based on the spatial evolution of an order parameter (which is related to the mass fraction of the phases) due to convection and diffusion, together with fluid flow. The interface between the phases is diffuse and is determined the gradient of the order parameter. Interfacial tension forces are calculated from the order parameter field, and are included in the fluid flow equations.
Illustration: Typical mixing in polymer processing
In order to illustrate the changing scales in mixing, consider a typical example in polymer processing where viscosities are on the order of 100 Pa·s and interfacial tension 0.005 N/m. Consider a typical screw with a diameter of 64 mm and a channel which can be approximated by the barrel wall moving over a cavity with dimensions 3 mm by 30 mm. If the screw rotates at 60 rpm, the relative speed of the upper wall to the screw is 0.2 m/s. A characteristic length scale for changes in velocity is around 3 mm and a typical initial value for ds is 1 mm. Using these typical values gives an initial capillary number of Ca ~ 1300, which clearly demonstrates that interfacial tension is unimportant in the initial stages of mixing. Interfacial tension stress does not become significant, Ca = O(1), until the striation thickness is reduced to about 10-5 m (10 mm).
Illustration: Role of dispersed phases on flow structure
Dispersed fluid phases which have properties different from the continuous phase can disrupt the structure of chaotic and regular regions obtained for single phase mixing. Zhang and Zumbrunnen (1996a) studied the patterns of mixing of a tracer in a time periodic cavity flow with and without a dispersed phase blob. The capillary number for the flow with the blob is small enough so that the blob does not deform significantly in the flow. The presence of the blob disturbs the flow in a random fashion when it is placed in the chaotic region, and thus eliminates islands by breaking KAM surfaces. From a macroscopic viewpoint, dispersed phases improve mixing. Put in another way, once some breakup has been achieved, further mixing becomes more efficient.
Small Scales
As the mixing proceeds, the capillary number decreases. At Ca=O(1), interfacial tension stresses become of the same order of magnitude as viscous stresses, and the extended thread breaks into many smaller drops. Large drops, corresponding to Ca>>1, may stretch and break again, while smaller drops begin to collide with each other and coalesce into larger drops, which may in turn break again.
To a first approximation, the velocity field with respect to a frame fixed on the drop's center of mass, denoted X, and far away from it, denoted by the superscript ¥, can be approximated by
![]() (A.6)
(A.6)
where
L=L(X,t)=(D+W) is a function of
the fluid mechanical path of the drop, and D and W are defined
as ![]() and
and ![]() , respectively. The central
point is to investigate the role of L in the stretching and breakup of
the drop.
, respectively. The central
point is to investigate the role of L in the stretching and breakup of
the drop.
As before, the problem is governed by the creeping flow equations and boundary conditions given earlier (eqs. (A.1)-(A.4)). The far field boundary condition in this case is
The tensor L defines the character of the flow. The capillary number for the drop deformation and breakup problem is
where R is the radius of the initially
spherical drop, and ![]() is the shear rate.
is the shear rate.
Experimental studies of drop breakup have been mainly confined to linear, planar flows. All linear flows in 2D are encapsulated by the following general velocity field equations:
where K determines the vorticity of the flow and G is a measure of the shear rate. Planar extensional flow corresponds to K=1 (zero vorticity) and simple shear flow corresponds to K=0. Streamlines for the flows with different values of K are shown in Figure 13. Uniaxial extensional flow is another common flow type encountered, and is defined by
For comparison of the different flows, it is necessary to define a consistent shear rate for all the flows. A natural choice is
This definition gives ![]() when applied to a simple shear flow
(i.e., K=0).
when applied to a simple shear flow
(i.e., K=0).
Flows may be classified as strong or weak (Giesekus, 1962; Tanner, 1976) based on their ability to stretch material elements after long times of stretching, and this characteristic can be inferred from the velocity field. Flows which produce an exponential increase in length with time are referred to as strong flows and this behavior results if the symmetric part of the velocity gradient tensor (D) has at least one positive eigenvalue. For example, 2D flows with K>0 and uniaxial extensional flow are strong flows; simple shear flow (K=0) and all 2D flows with K<0 are weak flows.
The degree of deformation and whether or not a drop breaks is completely determined by Ca, p, the flow type and the initial drop shape and orientation. If Ca is less than a critical value, Cacrit, the initially spherical drop is deformed into a stable ellipsoid. If Ca is greater than Cacrit a stable drop shape does not exist, so the drop will be continually stretched until it breaks. For linear, steady flows, the critical capillary number, Cacrit, is a function of the flow type and p. Figure 14 shows the dependence of Cacrit on p for elongational flow and simple shear flow. Bentley and Leal (1986) have shown that for flows with vorticity between simple shear flow and planar elongational flow, Cacrit lies between the two curves in Figure 14. The important points to be noted form Figure 14 are:
· It is easiest to stretch drops when p » 1.
· Elongational flow is more effective than simple shear flow for a given viscosity ratio.
Affine Deformation
For Ca > Cacrit a drop continually stretches until it breaks. If Ca > kCacrit where k is about 2 for simple shear flow and 5 for elongational flow (Janssen, 1993), the drop undergoes affine deformation, i.e., the drop acts as a material element, and it is stretched into an extended cylindrical thread with length L and radius R according to
Simple shear flow: ![]() ,
, ![]() (A.12)
(A.12)
Extensional flow: ![]() ,
, ![]() (A.13)
(A.13)
These expressions approach an exact equality as ![]() becomes large. Figure 15 illustrates the point
that a highly stretched drop can be treated as a material element (i.e.
it deforms affinely). This figure shows computations and experiments done by
Tjahjadi and Ottino (1991) where a drop of fluid is dispersed in a second fluid
in a vortex mixing flow, also referred to as the journal bearing flow. In the
computations, the drop was treated as a material element and as can be seen the
agreement between the computations and experiments is quite good. A necessary
condition for stretching is that Ca must surpass Cacrit as
illustrated in Figure 16: one drop does not reach the critical Ca and remains
undeformed, the other breaks into thousands of drops.
becomes large. Figure 15 illustrates the point
that a highly stretched drop can be treated as a material element (i.e.
it deforms affinely). This figure shows computations and experiments done by
Tjahjadi and Ottino (1991) where a drop of fluid is dispersed in a second fluid
in a vortex mixing flow, also referred to as the journal bearing flow. In the
computations, the drop was treated as a material element and as can be seen the
agreement between the computations and experiments is quite good. A necessary
condition for stretching is that Ca must surpass Cacrit as
illustrated in Figure 16: one drop does not reach the critical Ca and remains
undeformed, the other breaks into thousands of drops.
The stretching rate of long filaments in shear flow can be improved from being linear to exponential by incorporating periodic reorientations in the flow, as seen earlier for material lines. The basic idea is instead of using one long shear flow to divide the flow into shorter sections with reorientations between each section. When this is done the amount of stretching is given by (Erwin, 1978).
where gtot is the total shear in the mixer.
The improvement with reorientations is illustrated in Figure 17, where Ro/R is plotted versus time for the cases of 0, 2, 3, and 4
reorientations. After a total shear of 300 (![]() = 50 s-1 for 6
seconds), the length scale is reduced from 10-3 m to
6´10-5 m. If a reorientation is added after every two seconds, the
length scale is reduced from 10-3 m to 10-6 m (a typical length scale reduction in polymer processing). To
get this same reduction without reorientation would take approximately 5 1/2
hours. Four or five reorientations are typically enough.
= 50 s-1 for 6
seconds), the length scale is reduced from 10-3 m to
6´10-5 m. If a reorientation is added after every two seconds, the
length scale is reduced from 10-3 m to 10-6 m (a typical length scale reduction in polymer processing). To
get this same reduction without reorientation would take approximately 5 1/2
hours. Four or five reorientations are typically enough.
While the above equations illustrate
clearly the role of reorientation in stretching, it should be noted that the
equations are valid only when the strain per period is large (![]() ). The length of the filament is
after n reorientations is in fact given by
). The length of the filament is
after n reorientations is in fact given by
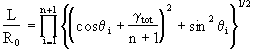 (A.15)
(A.15)where qi is
the angle between the filament and the streamlines at the start of the ith period (Khakhar and Ottino, 1986a). For large ![]() eq. (A.15) reduces to eq.
(A.14). However, when this condition is not satisfied, actual strains may be
less than or greater than unity depending on the orientation of the material
element (qi). Consequently, eq. (A.14)
would not give an accurate estimate of the optimum number of reorientations when
the length stretch is maximum.
eq. (A.15) reduces to eq.
(A.14). However, when this condition is not satisfied, actual strains may be
less than or greater than unity depending on the orientation of the material
element (qi). Consequently, eq. (A.14)
would not give an accurate estimate of the optimum number of reorientations when
the length stretch is maximum.
Illustration: Stretching of low-viscosity-ratio elongated drops
For the case p<<1 and Ca/Cacrit=O(1), the dynamics of a nearly axisymmetric drop with pointed ends, characterized by an orientation m (|m|=1) and a length L(t), is given by (Khakhar and Ottino, 1986b,c)
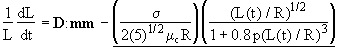 (A.16a)
(A.16a)
![]() (A.16b)
(A.16b)
where G(t)=(1+12.5R3/L(t)3)/(1-2.5R3/L(t)3). The underlined term in the first equation acts as a resistance to the deformation [contrast equation (A.16a) with equation (4) for stretching of a material element]. A very long drop, (L(t)/a)®¥, G®1, rotates and stretches as a passive element since the resistance to stretching becomes negligible. Note also that since G>1 the droplet "feels" a flow which is slightly more extensional than the actual flow. The above equation is a special case of the linear vector model (Olbricht et al., 1982) which describes the dynamics of deformation of an arbitrary microstructure which is specified by its length and orientation. We shall show later in this paper that the fragmentation and separation of agglomerates is also described by an equation very similar to the above equation.
In the context of the above model, a drop is said to break when it undergoes infinite extension and surface tension forces are unable to balance the viscous stresses. Consider breakup in flows with D:mm constant in time (for example, an axisymmetric extensional flow with the drop axis initially coincident with the maximum direction of stretching). Rearranging equation (A.16), and defining a characteristic length R/p1/3, we obtain the following condition for a drop in equilibrium
![]() (A.17)
(A.17)
where Ls denotes the steady-state length and E=p1/6Ca. A graphical interpretation of the roots Ls is given in Figure 18. The horizontal line represents the asymptotic value of the efficiency (i.e., corresponding to dm/dt=0), which in three-dimensions is (2/3)1/2, and the value of the resistance is a function of the drop length for various values of the dimensionless strain rate E. For E<Ec there are two steady states: one stable and the other unstable. For E>Ec there are no steady states and the drop extends indefinitely.
Once a drop is subjected to a flow for which Ca > Cacrit, it stretches and breaks depending on the degree of deformation, the viscosity ratio and the flow type (see for example Figure 16). When a drop breaks it does so by one of the four mechanisms illustrated in Figure 19 (Stone 1994). These four mechanisms will be briefly discussed here. For more details, see reviews by Eggers (1997), Stone (1994), Rallison (1984) and Acrivos (1983).
Moderately extended drops (![]() , where Ro is
the radius of a spherical drop of the same volume) break by a necking
mechanism (Rumscheidt and Mason, 1961). In this type of breakup, the two ends of
the drop form bulbous ends and a neck develops between them. The neck
continuously thins until it breaks, leaving behind a few smaller drops between
two large drops formed from the bulbous ends. This necking mechanism generally
occurs during a sustained flow where Ca is relatively close to Cacrit. Little has appeared in the literature
on the number and size of drops formed upon breakage by necking. One general
observation is that the number of drops produced is less than 10 (Grace,
1972).
, where Ro is
the radius of a spherical drop of the same volume) break by a necking
mechanism (Rumscheidt and Mason, 1961). In this type of breakup, the two ends of
the drop form bulbous ends and a neck develops between them. The neck
continuously thins until it breaks, leaving behind a few smaller drops between
two large drops formed from the bulbous ends. This necking mechanism generally
occurs during a sustained flow where Ca is relatively close to Cacrit. Little has appeared in the literature
on the number and size of drops formed upon breakage by necking. One general
observation is that the number of drops produced is less than 10 (Grace,
1972).
The necking mechanism has also been investigated using theoretical and numerical techniques. The theoretical approach, based on small deformation analysis (Barthès-Biesel and Acrivos, 1973) for the case of low Ca or high p shows the formation of lobes on the drop for Ca >Cacrit. Numerical techniques (Rallison, 1981) for p=1 give similar results. The general conclusion is confirmation of the experimentally determined curve for Cacrit; the drops in this case may breakup rather than extend indefinitely.
Tipstreaming, in which small drops break off from the tips of moderately extended, pointed drops, is another mechanism for drop breakup, though not of much significance to the dispersion process. Tipstreaming is generally attributed to gradients in interfacial tension along the surface of the drop (De Bruijn, 1993), but the exact conditions at which tipstreaming occurs are not well known.
Relaxation of a moderately extended drop under the influence of surface tension forces when the shear rate is low, may lead to breakup by the end-pinching mechanism (Stone, Bentley and Leal, 1986 and Stone and Leal, 1989). For example, this type of breakup occurs if a drop is deformed past a critical elongation ratio, (L/Ro)crit, at Ca close to Cacrit and then the flow is stopped abruptly. The critical elongation ratio necessary for breakup once the flow is stopped is dependent on p with a minimum deformation around p=0.2-2, but is nearly independent of flow type (Stone et al., 1986). Smaller than critical elongations result in relaxation of the drop to a spherical shape. The relaxation of the drop in this case is driven by the surface tension stress generated by the ends of the extended drop. The high viscosities and low surface tensions encountered in polymer processing lead to high relaxation times for the drop, hence breakup by end-pinching may not occur to any significant effect in such systems. However, this mechanism would be the dominant mode of breakup in the emulsification of low viscosity liquids.
The three breakup mechanisms previously discussed occur for moderately extended drops, however when Ca >kCacrit the drop is stretched affinely and becomes a highly extended thread. The extended thread is unstable to minor disturbances and will eventually disintegrate into a number of large drops with satellite drops between the larger mother drops (see Figure 19). The driving force behind this process is provided by interfacial tension minimizing the surface area: all sinusoidal disturbances cause a decrease in surface area. However, only disturbances with a wavelength greater than the filament perimeter produce pressure variations along the filament (due to the normal stress boundary condition) that magnify the disturbance and lead to breakup. The analysis for how these disturbances grow depends on whether the thread is at rest or being stretched. Each of these two cases are considered below.
For the case of a thread at rest, the initial growth of a disturbance can be relatively well characterized by linear stability theory. In the initial stages, the deformation of the thread follows the growth of the fastest growing disturbance (Tomotika, 1935). Eventually the interfacial tension driven flow becomes non-linear leading to the formation of the smaller satellite drops (Tjahjadi, Stone and Ottino, 1992).
Although linear stability theory does not predict the correct number and size of drops, the time for breakup is reasonably estimated by the time for the amplitude of the fastest growing disturbance to become equal to the average radius (Tomotika, 1935).
The non-dimensional growth rate, Wm, is a unique function of the wavenumber and p. Kuhn (1953) estimated the magnitude of the initial amplitude of the disturbances (ao) to be 10-9 m based on thermal fluctuations. Mikami, Cox and Mason (1975) gave a higher estimate of 10-8 to 10-7 m.
For the case of a thread breaking during flow, the analysis is complicated by the wavelength of each disturbance being stretched along with the thread. This causes the dominant disturbance to change over time, which results in a delay of actual breakup. Tomotika (1936) and Mikami et al. (1975) analyzed breakup of threads during flow for 3D extensional flow and Khakhar and Ottino (1987) extended the analysis to general linear flows. Each of these works uses a perturbation analysis to describe an equation for the evolution of a disturbance.
In general, disturbances will damp, then grow, and then damp again as the wavelength of a particular disturbance increases due to stretching of the thread. However, disturbances cannot damp below the initial amplitude, ao, caused by thermal fluctuations. Hence, the initial damping stage is omitted and once the thread reaches a critical radius, Rcrit, the disturbance starts to grow from ao. If the amplitude of a disturbance reaches the average size of the thread, disintegration into drops occurs. Disturbances grow and damp at different rates depending on their initial wave number xo. The disturbance which reaches the amplitude of the average thread radius first is the dominant disturbance and causes breakup.
Mikami et al. (1975) and Khakhar and Ottino (1987) presented a numerical scheme for determining tgrow, which is the time for the dominant disturbance to grow from ao to an amplitude equal to the average thread radius. The total breakup time, tbreak, is the sum of tgrow and tcrit, where tcrit is the time to reach Rcrit from Ro. The value of Rcrit is also obtained from the numerical scheme for calculating tgrow. Tjahjadi and Ottino (1991) used this numerical scheme and fitted the results to the following expression:
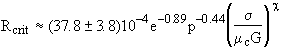 (A.19)
(A.19)where, 0.84 < c < 0.92 for ![]() . Janssen and Meijer (1993)
took the approach of Tjahjadi and Ottino (1991) one step further and reduced all
the results to a graphical representation of Rdrops, Rcrit, and tgrow which only depends on the
dimensionless parameters p and
. Janssen and Meijer (1993)
took the approach of Tjahjadi and Ottino (1991) one step further and reduced all
the results to a graphical representation of Rdrops, Rcrit, and tgrow which only depends on the
dimensionless parameters p and ![]() . The Illustration following this
section indicates how to calculate tbreak using these
graphs.
. The Illustration following this
section indicates how to calculate tbreak using these
graphs.
Although the area of breakup can be divided into four distinct categories -- necking, tipstreaming, end-pinching, and capillary instabilities -- more than one mechanism may be present in a given flow. Stone et al. (1986) and Stone and Leal (1989) demonstrated that if a drop is stretched enough both end-pinching and capillary instabilities will be present. The end-pinching mechanism dominates the breakup close to the ends and the capillary instabilities dominate the breakup of the drop towards the middle. An examination of the pictures of Tjahjadi and Ottino (1991) shows the presence of three breakup mechanisms; necking, end-pinching, and capillary instabilities on different portions of the same extended thread, however, capillary instabilities dominate the breakup.
Consider a thread being deformed in a 2D extensional flow, with the following material and process parameters.
![]()
![]()
![]()
![]()
![]()
![]()
Janssen and Meijer (1993) have shown the
calculation of the time for breakup of a thread during flow can be reduced to
the graphs in Figure 20, which only depend on the viscosity ratio, p=1, and the
parameter ![]() using
ao=
using
ao=![]() (Kuhn, 1953). Using these two parameters and Figure 20, the following values are
obtained
(Kuhn, 1953). Using these two parameters and Figure 20, the following values are
obtained
where, ![]() and
and ![]() .
Rcrit is the radius of the thread at which the fatal
disturbance begins to grow, Rdrops is the size of the drops
produced once the thread breaks, and tgrow is the time for
the disturbance to grow from its initial amplitude to half the average radius at
which breakup occurs. For ao=
.
Rcrit is the radius of the thread at which the fatal
disturbance begins to grow, Rdrops is the size of the drops
produced once the thread breaks, and tgrow is the time for
the disturbance to grow from its initial amplitude to half the average radius at
which breakup occurs. For ao=![]() , we obtain
, we obtain ![]() ,
, ![]() , and
, and ![]() . The time to reach Rcrit,
tcrit is found from the equation for stretching in a
2D exponential flow.
. The time to reach Rcrit,
tcrit is found from the equation for stretching in a
2D exponential flow.
Illustration: Satellite formation in capillary breakup
The distribution of drops produced upon disintegration of a thread at rest is a unique function of the viscosity ratio. Tjahjadi et al. (1992) showed through inspection of experiments and numerical simulations that up to 19 satellite drops between the two larger mother drops could be formed. The number of satellite drops decreased as the viscosity ratio was increased. In low viscosity systems (p<O(0.1)) the breakup mechanism is self-repeating: every pinch-off results in the formation of a rounded surface and a conical one; the conical surface then becomes bulbous and a neck forms near the end which again pinches off and the process repeats (Figure 21). There is excellent agreement between numerical simulations and the experimental results (Figure 21).
Illustration: Comparison between necking and capillary breakup
Consider drops of different sizes in a
mixture exposed to a 2D extensional flow. The mode of breakup depends on the
drop sizes. Large drops (![]() ) are stretched into long threads by the flow and undergo capillary
breakup, while smaller drops (
) are stretched into long threads by the flow and undergo capillary
breakup, while smaller drops (![]() ) experience breakup by necking. As a limit case, we consider necking
to result in binary breakup, i.e., two daughter droplets and no satellite
droplets are produced on breakup. The drop size of the daughter droplets is
then
) experience breakup by necking. As a limit case, we consider necking
to result in binary breakup, i.e., two daughter droplets and no satellite
droplets are produced on breakup. The drop size of the daughter droplets is
then
The radius of drops produced by capillary breakup is independent of the initial drop size, and is determined essentially by the viscosity ratio. Figure 22 shows a comparison of the drop size produced on breakup by the two different mechanisms (Janssen and Meijer, 1993). The size of the daughter drops produced by capillary breakup is significantly smaller than that for binary breakup for the case of high viscosity ratios. However, in practical situations in which coalescence and breakup occur during mixing, a range of drop sizes would exist, and thus the binary breakup radius gives an upper limit for the drop size.
Affinely deformed drops generate long filaments with a stretching distribution based on the log-normal distribution. The amount of stretching (l) determines the radius of the filament locally as
![]() (A.21)
(A.21)
Upon breakup, the filament breaks into a set of primary or mother drops whose sizes are, to a first approximation, proportional to R. The size of drops produced when the filament breaks can then be obtained from the distribution of R. Each mother drop produced upon breakup carries a distribution of satellites of diminishing size; for example each mother drop of radius r has associated with it one large satellite of radius r(1), two smaller satellites of radius r(2), four satellites of radius r(3), and so on. For breakup at rest, the distribution of smaller drops is a unique function of the viscosity ratio.
If we assume that drops break only once the drop-size distribution can be predicted based on the log-normal stretching distributions typical of mixing flows. Assuming a mean stretch of 104 gives a range of stretching from 1 to 1010 (Muzzio et al., 1991). Therefore, the corresponding distribution of mother drops is log-normal with a range from Ro to 10-5Ro, where Ro is the radius of the initial drop. The distribution for each satellite drop will be the same as that of the mother drop, except the position of the distribution will be shifted by a factor of r/r(i) and the amplitude multiplied by the number of satellite drops per mother drop. When all of the individual distributions are added, to give the overall drop distribution, a log-normal distribution is approached, as illustrated in Figure 23.
The above example, as well as the
repetitive nature of stretching and breakup, suggests that the experimentally
determined equilibrium drop size distribution f(V,p) might be self-similar
[f(V,p)dV is the number of drops with sizes between V and V+dV]. Figure 24 shows
the distribution of drops obtained experimentally in the journal bearing flow
resulting from repeated stretching and breakup. Figure 25 shows that re-scaled
experimental drop-size distributions V2f(V,p) vs. ![]() , where
, where ![]() is the arithmetic mean of volume
sizes collapses all data into a single curve.
is the arithmetic mean of volume
sizes collapses all data into a single curve.
Illustration: Effect of viscosity ratio on drop size distributions
Experiments show that the equilibrium size distributions corresponding to high-viscosity-ratio drops are more non-uniform than those corresponding to low viscosity ratios, and that, in general, the mean drop size decreases as the viscosity ratio p increases (Tjahjadi and Ottino, 1991). The experiments pertain to the case of low number densities of drops when coalescence is negligible. There seem to be two distinct mechanisms: one-time breakup and repeated-breakup. Low viscosity drops stretch passively but extend relatively little before they break resulting in the formation of large droplets; these droplets undergo subsequent stretching, folding, and breakup. Under identical conditions, high-viscosity-ratio drops stretch substantially, O(103-104), before they break producing very small fragments; these small fragments rarely break again. It is apparent, contrary to a long-held belief, that the finest dispersion does not correspond to p=1.
- The number of drops produced upon breakup by necking is generally less than 10.
- The time for breakup by necking increases with p.
- Breakup by end-pinching is most difficult for very viscous or inviscid drops.
- The size of daughter droplets produced is independent of the initial drop size.
- The number of satellite drops produced upon breakup by capillary instabilities decreases as p increases (minimum of 3 - maximum of 16).
- Breakup during flow is delayed relative to breakup at rest, so in general the easiest way to break an extended thread is to stop the flow.
- Viscosity ratio p=1 does not produce the finest dispersion; average drop sizes decrease with viscosity ratio.
Collisions
As dispersion proceeds drops come into close contact with each other and may coalesce. Coalescence is commonly divided into three sequential steps (Chesters, 1991): "collision", or close approach of two droplets, drainage of the liquid between the two drops, and rupture of the film (see Figure 26).
The collision frequency between drops may
be estimated by means of Smoluchowski?s theory (see, for example Levich, 1962).
The collision frequency (![]() number of collisions per unit time per unit volume) for randomly
distributed rigid equal-size spheres, occupying a volume fraction f, is given by:
number of collisions per unit time per unit volume) for randomly
distributed rigid equal-size spheres, occupying a volume fraction f, is given by:
where n is the number density of drops
(number per unit volume). Due to the fact that hydrodynamic interactions are
neglected, this equation gives at best an order of magnitude estimate for the
collision frequency. However, it is important to note that the result is
independent of flow type if ![]() is interpreted as
is interpreted as ![]() (see following
Illustration). The collision rate for small drops considering hydrodynamic
interactions is given in Wang, Zinchenko and Davis (1994). A thorough analysis
of coagulation in the presence of hydrodynamic interactions, interparticle
forces, and Brownian diffusion in random velocity fields is given by Brunk et
al. (1997).
(see following
Illustration). The collision rate for small drops considering hydrodynamic
interactions is given in Wang, Zinchenko and Davis (1994). A thorough analysis
of coagulation in the presence of hydrodynamic interactions, interparticle
forces, and Brownian diffusion in random velocity fields is given by Brunk et
al. (1997).
The collision frequency for a general linear flow (eq. A.5) is obtained following Smoluchowski's (1917) approach as (Bidkar and Khakhar, 1990)
in spherical coordinates (r,q,f), where ![]() is the collision radius
and m is the unit normal to the collision surface. If the coordinate axes
are chosen to be the principal axes, the tensor D is diagonal, with the
diagonal elements given by the roots of
is the collision radius
and m is the unit normal to the collision surface. If the coordinate axes
are chosen to be the principal axes, the tensor D is diagonal, with the
diagonal elements given by the roots of
where ![]() and
and ![]() . Thus, in the context of
Smoluchowski's theory, the only parameter that specifies the flow type
is
. Thus, in the context of
Smoluchowski's theory, the only parameter that specifies the flow type
is ![]() which has a
range of possible values
which has a
range of possible values ![]() . Clearly, vorticity plays no role in the process. For 2D
flows,
. Clearly, vorticity plays no role in the process. For 2D
flows, ![]() =0, so
that the collision frequency is independent of flow type and given by
=0, so
that the collision frequency is independent of flow type and given by
For general linear flows, the limit case
of axisymmetric flows (![]() =
=![]() )
gives
)
gives
The above results show that the Smoluchowski collision frequency is independent of flow type for planar flows and that the maximum collision frequency (obtained for axisymmetric flows) is only 5% larger than that for planar flows.
Once a "collision" occurs, the liquid between the drops is squeezed forming a film. As the drops are continually squeezed by the external flow field, the drops rotate as a dumbbell and the film drains. At some distance ho, the drops begin to influence each other and their rate of approach, dh/dt, decreases and is now governed by the rate of film drainage.
The rate of approach, dh/dt, is determined by the different boundary conditions of the interface, which characterize the mobility and rigidity of the interface. The mobility of the interface is essentially determined by the viscosity ratio and determines the type of flow occurring during film drainage. The rigidity of the interface is determined by the interfacial tension and determines the degree of flattening of the drop. These boundary conditions, along with the different expressions for dh/dt, are displayed in Figure 27 (Chesters, 1991).
The required time for complete film drainage is given by integrating the equations for dh/dt from ho to the critical film thickness at which film drainage ends and rupture begins. If the driving force for film drainage is taken, as a first approximation, to be the Stokes drag force acting on the drops
integrating dh/dt is straightforward. This is clearly a simplified picture, but consistent with the assumptions used for calculation of the collision rate (eq.(A.22)). A more accurate estimate of the force may be obtained from Wang et al. (1994). The film drainage times for the different boundary conditions are given in Figure 27. The expressions differ significantly particularly with regard to the dependence on the applied force (F) and initial separation (ho). In all cases, except for the perfectly mobile interface, the drainage time is directly proportional to the continuous phase viscosity (mc) and interfacial tension is important only in those cases where the drops are deformed. The equations in Figure 27 are based on the formation of a flat circular film between the drops of radius 'a', and this dimension can be calculated from the applied force.
If a critical film thickness is not reached during film drainage, the drops separate from each other. Conversely, if the critical film thickness is reached, the film ruptures -- as a result of van der Waals forces -- and the drops coalesce. This generally occurs at thin spots, because van der Waals forces are inversely proportional to h4 (Verwey and Overbeek, 1948). The value of hcrit can be determined by setting the van der Waals forces equal to the driving force for film drainage giving (Verwey and Overbeek, 1948)
![]() (A.28)
(A.28)
where H is the Hamaker constant.
A few general conclusions can be arrived from the equations presented in Figure 27. In general, the drainage time is shortest when the drops are rigid (top equation). Smaller drops are more likely to coalesce than larger ones because the drainage time decreases with drop size. Since the drainage time decreases with force in all cases except the fully mobile interface, coalescence is more likely in lower shear rate zones where the force is lower (eq. (A.27)). Furthermore, surfactants and high viscosity dispersed phases, both of which reduce the mobility of the interface, result in longer drainage times and thus lower probabilities of coalescence.
* Coalescence is unimportant for dispersed phase volumes fraction (f) less than about 0.02; the rate of coalescence increases with f.
* Smaller drops are more likely to coalesce, after collision, than larger drops.
* Coalescence is more likely to take place in regions of low shear rate
* Coalescence becomes more likely as the mobility of the interface increases.
There have been several attempts at models incorporating breakup and coalescence. Two concepts underlie many of these models: binary breakup and a flow subdivision into weak and strong flows. These ideas were first used by Manas-Zloczower, Nir and Tadmor (1982,1984) in modeling the dispersion of carbon black in an elastomer in a Banbury internal mixer. A similar approach was taken by Janssen and Meijer (1995) to model blending of two polymers in an extruder. In this case the extruder was divided into two types of zones, strong and weak. The strong zones correspond to regions of high shear with short residence times, where stretching of drops into threads and breakup of threads during flow takes place. The weak zones correspond to regions of low shear and long residence times, where breakup of threads at rest and coalescence of drops occurs. Janssen and Meijer (1995) modeled the strong zone as elongational flow and the weak zone as simple shear flow. After each zone, conditions were checked for stretching, capillary breakup, and coalescence according to local coalescence and breakup theory. An initial drop size distribution was passed through a series of alternating strong and weak zones a specific number of times resulting in a final drop size distribution. Using this model the effects of material properties and process parameters on the final drop size distribution were evaluated. Another model was proposed by Huneault, Shi and Utracki (1995) again, to model dispersion in extruders. In this case however, a simplified flow analysis was used to model the flow in the extruder which gave estimates for the average values of Ca. According to the average Ca in each zone, the average drop diameter was evolved according to a number of rules which included binary breakup. The droplet size distribution in simple shear flow was studied by Patlazhan and Lindt (1996) using a population balance approach based on simple models to predict droplet breakage and coalescence rates.
Let us consider the so-called Viscous Immiscible Liquid Mixing (VILM) model (DeRoussel, 1997). This model incorporates most of the important physical processes occurring during drop breakup described in the previous sections, though simplifications are inevitable. The basic approach is similar to that of Janssen and Meijer (1995) - a strong zone modeled by elongational flow in which stretching and breakup by capillary instabilities during flow occur and a weak zone modeled by shear flow in which coalescence and breakup by capillary instabilities at rest occur. The physical aspects of the VILM model which are not included in the model of Janssen and Meijer are summarized below
* Strong and weak zones are divided into sub-zones which allow for a distribution of shear and elongation rates and residence times.
* Threads breaking by capillary instabilities break into a distribution of drops rather than drop sizes of equal size.
* Coalescence between drops of different size is allowed.
* Variation of the driving force during film drainage is taken into account.
The elongation rates for each of the sub-zones in the strong zone are chosen so that the amount of stretching incurred matches a given stretching distribution. So, if stretching distributions are known for a given mixer, a connection can be made between the relatively simple parameters of the VILM model and the complex flow of the mixer. Techniques for determining the stretching distributions in a mixer are addressed in Muzzio, Swanson, and Ottino (1991) and Hobbs and Muzzio (1997).
Computations for the weak zone are carried out in discrete time steps with the time step taken to be the average time between collisions, as given by Smoluchowski's theory (equation (A.22)). At each time step, the following procedure is performed. Two drops are chosen at random and placed in a collision array along with the time the collision occurred and the drainage time for these two particular drops. Each extended thread is checked to see if it has been at rest long enough for breakup due to capillary instabilities to occur. If enough time has elapsed for the thread to break, the corresponding number of drops replaces the thread. The collision array is checked to see if any of the drop pairs have been in contact long enough for the film to drain. When sufficient time has elapsed, the two colliding drops coalesce to form a single larger one. At the end of the time in the weak zone, all drop pairs remaining in the collision array are returned to the drop general population and the next cycle or sub-zone is started.
The above procedure requires a calculation of the drainage time for each collision. When the number of collisions which occur during a single pass through the weak zone becomes large, O(107), the above procedure takes too long and is no longer practical. In order to deal with this complication, the number of drops is reduced by a factor which gives a feasible collision frequency. The shape of the distribution is preserved when the number of drops is reduced, so nothing is lost in the simulation.
By using the above procedure, the VILM model allows general trends to be found as process and material parameters are varied. Figure 28 shows the results of a typical simulation in which an initial drop distribution passes through a number of cycles until a steady-state is reached after six cycles. An important point to note is that after five cycles the resulting distribution is at a smaller size than the final distribution. This phenomena is referred to as overemulsification in the emulsion technology literature (Becher and McCann, 1991), but apparently has not been documented in polymer processing. Overemulsification is a result of the many small satellite drops produced by capillary breakup. The mean drop size then increases with time because the small drops cannot break further and coalescence dominates. Thus breakup dominates the early part of the process and coalescence dominates the later stages of mixing.
One variable which is commonly used to "classify" the morphology of a blend is the viscosity ratio. Quite often the average drop size is given as a function of the viscosity ratio. Figure 29 gives the results of a number of simulations in which the average size is plotted versus the viscosity ratio for different continuous and dispersed phase viscosities. As can be seen from this figure, for a given viscosity ratio the average size can vary a great deal. Hence it is the values of each viscosity, dispersed and continuous, and not just the viscosity ratio which is important in determining the average size. In addition, the average size increases sharply with decrease in the continuous phase viscosity for a fixed dispersed phase viscosity, while the average size is nearly constant for a fixed continuous phase viscosity when the dispersed phase viscosity is varied over 3 orders of magnitude.
* The average drop size increases with decrease in continuous phase viscosity.
* Intermediate mixing times may produce the smallest drops; long mixing times result in an equilibrium size which is larger.
PHYSICAL PICTURE
Powders dispersed in liquids consist of agglomerates -- a collection of aggregates -- which in turn are composed of primary particles. Agglomerates break due to flow; aggregates do not. Often these particles are of colloidal size, with a size ratio agglomerates/aggregates of about 103. In the case of carbon black, for example, aggregates are of the order of 0.1 mm and agglomerates are of the order of 10-100 mm and larger. Thus the length reduction in solid dispersion is about of the same order of magnitude as in dispersion of liquids. Often we will refer to both aggregates and agglomerates as clusters, a cluster being composed of particles. The size of a cluster is given by the number of particles composing the cluster.
The objective of mixing -- or dispersion -- of solids is to break agglomerates to aggregate size, the process giving rise to broad, time evolving cluster size distributions. The entire process of dispersion of a powder into a liquid involves several stages, which may all be occurring with some degree of overlap. Several scenarios have been proposed and, unavoidably, a proliferation of terms have ensued. For instance, Parfitt's (1992) scenario consists of four stages: Incorporation is the initial contact of the solid with the medium. Wetting, which follows incorporation, may in turn consist of: (i) adhesion of the medium to the solid, (ii) immersion of the solid into the fluid, and (iii) spreading of the liquid into the porous solid. Breakup (or fragmentation) and flocculation (or aggregation) conclude the dispersion process. A much narrower definition of dispersion: is commonly used in the polymer processing literature: fragmentation of agglomerates into aggregates, and the distribution of the aggregates into the medium.
In fact, the term fragmentation is commonly used in the physics literature to refer to a broader class of processes involving breakup of solids, such as rocks. Much of this literature can be adapted, mutatis mutandi, to the dispersion of agglomerates as is of interest here (see Figure 1). Fragmentation may be in turn divided into two modes of breakup (Redner, 1980): rupture and erosion; rupture referring to the breakage of a cluster into several fragments of comparable size, erosion to the gradual shearing off of small fragments from larger clusters (Figure 30). The main qualitative difference between these two mechanisms is energy input: low for erosion, high for rupture. Erosion dominates dispersion when stresses are low. Finally, materials may shatter producing a large number of smaller fragments in a single event as in the case of high energy fragmentation. While the physical mechanisms may be different, there are similarities between fragmentation of solids, and breakup of liquid drops at least with respect to the size distribution of fragments produced on breakup: Tip streaming is analogous to erosion, necking to rupture, and capillary breakup to shattering.
Aggregation (flocculation is the term commonly used in the rubber industry) may be imagined as being the reverse of dispersion. Aggregates come together, interact via hydrodynamic forces and particle potentials, and eventually bind. Two bonding levels are possible: strong and weak; strongly bound aggregates can not be redispersed by future stirring; weakly bonded aggregates can be dispersed by stirring. As opposed to coalescence of droplets, structure in this case may be preserved and fractal-like structures (Figure 31) are common. The mass of such clusters increases with radius according to RD rather than R3 for compact agglomerates, where D<3 is the fractal dimension. As we shall see, flows can in fact be manipulated to tailor structures.
SMALL SCALES: PARTICLE INTERACTIONS
The current level of understanding of how aggregates form and break is not up to par with droplet breakup and coalescence. The reasons for this discrepancy are many; aggregates involve multibody interactions, shapes may be irregular, potential forces which are imperfectly understood and quite susceptible to contamination effects.
Thus analyses of how aggregates break have resorted to idealizations inspired by traditional fluid mechanical analysis, two limit cases being permeable and impermeable spheres. Quite possibly the simplest model is to regard an agglomerate as a pair of bound spheres. As in the case of drop breakup the analysis considers scales such that the surrounding flow is linear. The velocity of one particle relative to the other, taking into account hydrodynamic and potential interactions between the two particles, is
![]() (B.1)
(B.1)
where r is a vector joining the centers of the two spheres, D is the rate of strain tensor, w is the vorticity of the driving flow, A(r) and B(r) are known functions (Batchelor and Green, 1972), and I is the identity matrix. In the last term, Fc is the physicochemical force between the particles, m is the fluid viscosity, R is the radius of the particles, and C(r) is a parameter which accounts for the particle proximity effect on drag (Spielman, 1970). The first three terms in the above equation give the relative velocity between the spheres in a linear flow field under the influence of hydrodynamic interactions, and the last term gives the relative velocity due to the physicochemical forces between the spheres. Rupture of this idealized aggregate occurs if hydrodynamic forces overcome the binding physicochemical forces as we show below. The above equation also applies to the analysis of the aggregation of initially separated particles in a linear flow (Zeichner and Schowalter, 1977).
The physicochemical forces between colloidal particles are described by the DLVO theory (DLVO refers to Derjaguin and Landau, and Verwey and Overbeek). This theory predicts the potential between spherical particles due to attractive London forces and repulsive force due to electrical double layers. This potential can be attractive, or both repulsive and attractive. Two minima may be observed: The primary minimum characterizes particles which are in close contact and are difficult to disperse, while the secondary minimum relates to looser dispersible particles. For more details see Schowalter (1984). Undoubtedly, real cases may be far more complex: many particles may be present, particles are not always the same size, and particles are rarely spherical; however, the fundamental physics of the problem are similar. The incorporation of all these aspects into a simulation involving tens of thousands of aggregates is daunting and models have resorted to idealized descriptions.
There is a large body of theoretical work dealing with fragmentation. General aspects, primarily in the context of mathematical aspects of particle size distributions produced on fragmentation, are covered by Redner (1990) and Cheng and Redner (1990) whereas a review of various modeling approaches and experimental results, addressing grinding of solids, is presented by Austin (1971). Of special interest is the distribution of fragments upon rupture. Power law forms for cumulative distributions based on particle radius are commonly obtained and, in many cases, the distribution of fragments produced in a single rupture event is homogeneous (i.e., the distribution depends only on the ratio of the mass of the fragment of the mass of the original particle). Erosion produces fragments much smaller than the original particle and consequently the particle size distribution is bimodal. This body of literature provides a starting point for the understanding of the dispersion of agglomerates in viscous flows (Figure 30).
Fragmentation of agglomerates is similar to rupture of solids in that both agglomerates and granular solids deform only slightly before breaking. Differences arise mainly from the complex internal structure of agglomerates. In addition, the weaker bonding in agglomerates results in fragmentation at relatively low stresses. Fragmentation may be caused by several mechanisms, for example, application of direct compressive loads and particle-particle and wall-particle impacts. However, here we focus only on fragmentation by hydrodynamic forces which is of most relevance to polymer processing. By analogy with liquid droplets and the capillary number (equation A.8) the dimensionless parameter that characterizes the fragmentation process is the ratio of the viscous shear stress to the strength of the agglomerate. We term tthis ratio the Fragmentation number, Fa:
The term T denotes the characteristic cohesive strength of the agglomerate and plays a role analogous to the surface tension stress (s/R) in the definition of the Capillary number for liquid drops. Unlike surface tension, however, the agglomerate strength is not a material property but depends on internal structure, density (degree of compaction), moisture and many other variables. A similar definition of a dimensionless Fragmentation number appears in previous studies (e.g., Rwei, Manas-Zloczower and Feke, 1990) though not termed as such.
Agglomerate strength
The cohesive strength of an agglomerate owes its origins to interparticle bonds due to electrostatic charges, van der Waals forces, or moisture. Experimental methods for the measurement of the characteristic agglomerate strength include the tensile testing of compacted pellets (Rumpf, 1962; Hartley and Parfitt, 1984), notched bending tests of compacted beams (Kendall, 1988) and compression testing of compacted beds by penetration of a conical tester (Lee, Feke and Manas-Zloczower, 1993). The three tests measure different properties: the tensile strength, the tensile strength in the presence of flaws and the cohesivity, respectively. Values obtained from different test methods for the same agglomerate would clearly be different; trends with changes in parameters are, however, similar.
Two idealized models have been reasonably successful in predicting the strength of agglomerates and we review them here. Rumpf (1962) assumed the agglomerates to be spatially uniform and composed of identical spheres of radius 'a' bound to touching neighbors by van der Waals forces. Considering a planar rupture surface, the tensile strength T is
where H is the Hamaker constant,
f is the
solids volume fraction and ![]() is the equilibrium separation distance between the sphere surfaces.
Kendall (1988), on the other hand, used the Griffith criterion for crack growth
to obtain
is the equilibrium separation distance between the sphere surfaces.
Kendall (1988), on the other hand, used the Griffith criterion for crack growth
to obtain
where G is the interfacial
energy, Gc is the fracture energy, and
c is the initial length of the crack (edge notch). The two mechanisms, fracture
at a plane and crack growth, give very different expressions, particularly with
respect to dependence on the solids volume fraction (f) and the aggregate
(primary particle) radius (a). Surprisingly, agglomerates may rupture by either
of these mechanisms. For example, experiments using titanium dioxide
agglomerates carried out by Lee, Feke and Manas-Zloczower (1993) found
the strength of agglomerates (![]() mm)
to follow Rumpf's model whereas Kendall (1988) found the agglomerates (
mm)
to follow Rumpf's model whereas Kendall (1988) found the agglomerates (![]() mm) to follow the crack growth model.
A notable difference was the order of magnitude lower strength measured by Lee
et al. (1993) as compared to the agglomerates of Kendall (1988), however,
this may be due to the different test methods used.
mm) to follow the crack growth model.
A notable difference was the order of magnitude lower strength measured by Lee
et al. (1993) as compared to the agglomerates of Kendall (1988), however,
this may be due to the different test methods used.
The nature of the local flow significantly affects the separation of fragments produced on rupture of an agglomerate, as shown by Manas-Zloczower and Feke (1988), for equal sized spherical fragments. Significantly higher shear rates are required for separation in a simple shear flow as compared to extensional flows. As the following analysis demonstrates, the process of separation is very similar to the breakup of slender drops (Khakhar and Ottino, 1986b,c; Ottino, 1989); thus previous results are useful for generalizing the analysis of fragment separation for all linear flows.
The spherical fragments, initially in close contact, move relative to each other according to equation (B.1). The underlying physics is revealed more clearly by recasting equation (B.1) in the following dimensionless form
![]() (B.5)
(B.5)
Here r is the center-to-center
distance, and m is a unit vector along the line joining the centers of
the two fragments, so that r=rm. Distances are made dimensionless
with respect to the radius of a fragment (a), shear rates and time with respect
to the characteristic shear rate ![]() , and Fc=|Fc| with respect to
H/a. The above equations are identical in form to those for the breakup
for a slender drop (Khakhar and Ottino, 1986b) discussed earlier.
, and Fc=|Fc| with respect to
H/a. The above equations are identical in form to those for the breakup
for a slender drop (Khakhar and Ottino, 1986b) discussed earlier.
Several conclusions result from the above equations: They reveal that the dimensionless parameter of the system is the fragmentation number (Fa) with the characteristic strength given by
The rate of separation of the fragments depends on the functions A(r), C(r), Fc, and the fragmentation number, while the rate of rotation depends only on the function B(r). Further, it is apparent that the separation between the fragments increases only when the hydrodynamic force exceeds the binding physicochemical force. The pair of fragments rotates as a material element in an apparent flow with an effective velocity gradient tensor
Since B is positive the apparent flow appears to have a higher vorticity relative to the strain rate than the imposed flow.
Based on the above discussion, a criterion for the separation of the fragments is easily obtained. If at least one eigenvalue of the tensor M is positive, the pair orients along the corresponding principal axis, and the critical Fragmentation number for separation is given by
where ![]() is the asymptotic value of
is the asymptotic value of ![]() (i.e., the largest
positive eigenvalue of M), and
(i.e., the largest
positive eigenvalue of M), and ![]() is the equilibrium separation.
For
is the equilibrium separation.
For ![]() the fragments separate indefinitely. In arriving at the above
equation the physicochemical force was estimated for a pair of equal sized
spheres as Fc=1/12zo2 (Rumpf, 1962),
and the result
the fragments separate indefinitely. In arriving at the above
equation the physicochemical force was estimated for a pair of equal sized
spheres as Fc=1/12zo2 (Rumpf, 1962),
and the result ![]() for small separations was used. Special cases of this result were presented by
Manas-Zloczower and Feke (1988). For purely extensional flows (W=0), we
have
for small separations was used. Special cases of this result were presented by
Manas-Zloczower and Feke (1988). For purely extensional flows (W=0), we
have ![]() for planar
flows and
for planar
flows and ![]() for
axisymmetric flows. In the case of simple shear flow, eigenvalues are imaginary,
hence no asymptotic orientation exists and the separation distance oscillates
with time as the fragments rotate in the flow. Separation of fragments in this
flow occurs, according to Manas-Zloczower and Feke (1988) when the potential
energy due to the van der Waals force at the maximum separation distance is less
than the thermal energy. This criterion gives the critical separation as
for
axisymmetric flows. In the case of simple shear flow, eigenvalues are imaginary,
hence no asymptotic orientation exists and the separation distance oscillates
with time as the fragments rotate in the flow. Separation of fragments in this
flow occurs, according to Manas-Zloczower and Feke (1988) when the potential
energy due to the van der Waals force at the maximum separation distance is less
than the thermal energy. This criterion gives the critical separation as
where kB is the
Boltzmann constant. The critical fragmentation number for separation should be
at least as large as that for planar extension; numerical simulation is required
to obtain ![]() at
which the criterion z>zc is
satisfied.
at
which the criterion z>zc is
satisfied.
Agglomerates in a sheared fluid rupture when the hydrodynamic stress exceeds a critical value; in dimensionless form the criterion for rupture is Fa>Facrit. Rupture occurs within a short time of application of the critical stress, and thus can be distinguished from erosion which occurs over much longer time scales.
Experimental data for the critical
fragmentation number is sparse and certainly much less than what is available
for droplets. Rwei, Manas-Zloczower and Feke (1990) carried out experiments to
determine the critical stress for the rupture of compact agglomerates in simple
shear flow. Carbon black pellets of different densities (r) and silicone oils of
different viscosities were used. The tensile strength of the agglomerates was
measured and is well correlated by Kendall's (1988) model: T?Kr4
with ![]() Pa
(g/cm3)-4. The critical shear stress
applied at the point of rupture was found to be
Pa
(g/cm3)-4. The critical shear stress
applied at the point of rupture was found to be ![]() with
with ![]() Pa (g/cm3)-4 for the different density pellets and the fluids of varying
viscosity. The reported data thus gives Facrit? 0.05
independent of pellet density. The dependence of Facrit on
the agglomerate size was not studied. (Note: the magnitude of Facrit depends on the method used for measuring the strength of the
agglomerate, T.) The size distribution of the fragments formed upon rupture is
log-normal. This seems to be in agreement with the theory for random breakage
discussed later in this section.
Pa (g/cm3)-4 for the different density pellets and the fluids of varying
viscosity. The reported data thus gives Facrit? 0.05
independent of pellet density. The dependence of Facrit on
the agglomerate size was not studied. (Note: the magnitude of Facrit depends on the method used for measuring the strength of the
agglomerate, T.) The size distribution of the fragments formed upon rupture is
log-normal. This seems to be in agreement with the theory for random breakage
discussed later in this section.
Rupture of fractal (flocculated) aggregates of polystyrene latices in simple shear flow and converging flow was studied by Sonntag and Russel (1986,1987b). For simple shear flow and low electrolyte concentrations, the critical fragmentation number decreases sharply with agglomerate radius (R) as
where the agglomerate strength, T=595 dynes/cm2, is obtained by fitting a theory (discussed below) to the experimental data. The fractal dimension of the agglomerates is D?2.5. Ionic effects at high electrolyte concentrations are well accounted for by assuming T to be proportional to the force between two primary particles calculated using the DLVO theory (the bond strength between the primary particles increases with increasing ionic strength). In the converging flow, the mass of the critical agglomerates decreases linearly with increasing shear rate like the shear flow, but the radius of gyration is nearly constant. Such behavior could be due to the formation of elongated fragments upon rupture.
Theoretical prediction of the critical fragmentation number requires an estimate of the hydrodynamic stress acting on the agglomerate. For the case of spherical impermeable agglomerates Bagster and Tomi (1974) showed that rupture in simple shear flow occurs on a plane through the center of the agglomerate, and Facrit is independent of the agglomerate size. In the analysis, the hydrodynamic stress on the surface is given by
(Brenner, 1958). Feke and Manas-Zloczower (1991) extended this analysis to the case of spherical agglomerates with a single flaw considering rupture to occur by crack growth. Again Facrit is independent of size. A significant result is that rupture is more likely in simple shear flow, as compared to extensional flows since the agglomerate rotates in a simple shear flow and the rupture surface (flaw) experiences the entire range of stresses possible.
The case of permeable porous agglomerates gives qualitatively different results. Adler and Mills (1979) showed that Facrit decreases with agglomerate size initially, but approaches the impermeable limit for large agglomerates (R/k1/2 >> 1, where m/k is the permeability). Sonntag and Russel (1987a) analyzed fractal structures using a similar approach. The fractal structure is incorporated into the mean field approach by considering a radially varying solids volume fraction
with the strength given by T=Kfn (similar to Kendall's model). This model predicts the experimentally determined dependence of Facrit on agglomerate size when n=4.45 (Figure 32). In both the models for porous agglomerates, hydrodynamic stresses within the sphere are calculated using the Brinkman equation with creeping flow in the surrounding fluid. The Mises rupture criterion
is used in both analyses, where
TD is the deviatoric part of the stress tensor
(i.e. ![]() ). Thus
rupture can occur at any point in the sphere.
). Thus
rupture can occur at any point in the sphere.
Most recently, Horwatt, Manas-Zloczower and Feke (1992,1993) carried out a numerical study of the rupture of fractal clusters generated by different aggregation protocols (more details of these protocols are given in § Aggregation). The clusters are modeled as impervious spheres and the hydrodynamic force is calculated following the approach of Bagster and Tomi (1974). The cluster ruptures if the resultant stress on the bonds between clusters exceeds a specified bond strength. The critical fragmentation number decreases with agglomerate radius for clusters with low fractal dimension (D) and is nearly independent of cluster size for compact clusters. This is in agreement with previous theories. The magnitude of Facrit, however, does not seem to have a strong correlation with the fractal dimension of the cluster.
EROSION
Erosion of agglomerates due to hydrodynamic stresses occurs over long time scales and at low values of the fragmentation number (Fa<<Facrit). The fragments eroded are much smaller than the parent particle (volume of fragment < 10% of volume of parent). Of primary interest from the viewpoint of dispersion of agglomerates is the rate of erosion and the size distribution of eroded fragments. Only a few studies focusing on these aspects have been carried out, and we summarize the main results here.
Erosion kinetics for compact spherical structures are well described by
at short times of erosion, where R is the
radius of the parent agglomerate, R0 is the initial radius,
and ke is a dimensionless erosion rate constant. The above
equation implies that the rate of erosion (volume eroded per unit time) is
directly proportional to the surface area of the parent. Thus ke is a first order rate constant, and for long times ![]() .
.
In the case of compact cohesionless
clusters (no attractive forces between aggregates forming agglomerate)
Powell and Mason (1982) found ke to be independent of shear
rate but dependent on flow type and the ratio (a/R0), where
a is the radius of the primary particle (aggregate). In contrast, Rwei,
Manas-Zloczower and Feke (1991) in a study of compact carbon black agglomerates
in simple shear flow found ke to depend only on the
fragmentation number (Fa) based on experiments carried out at different shear
rates and pellet densities (Figure 33). The critical shear rate below which
erosion stops was found to be ![]() Pa by extrapolating data obtained at
different stresses to a zero erosion rate. Using the strength of agglomerates
determined in their earlier work (Rwei et al., 1990) the critical
fragmentation number for erosion is obtained as
Pa by extrapolating data obtained at
different stresses to a zero erosion rate. Using the strength of agglomerates
determined in their earlier work (Rwei et al., 1990) the critical
fragmentation number for erosion is obtained as ![]() which is an order of magnitude
lower than Facrit. The size (radius) distribution of the
fragments was found to be Gaussian with a mean and standard deviation
proportional to the initial radius of the parent. In a separate study, carried
out at significantly higher values of Fa, Rwei, Manas-Zloczower and Feke (1992)
found the radius to decrease exponentially with time.
which is an order of magnitude
lower than Facrit. The size (radius) distribution of the
fragments was found to be Gaussian with a mean and standard deviation
proportional to the initial radius of the parent. In a separate study, carried
out at significantly higher values of Fa, Rwei, Manas-Zloczower and Feke (1992)
found the radius to decrease exponentially with time.
Physicochemical interaction between the agglomerate and fluid is an additional factor which affects the rate of erosion. For example, in a study of erosion under simple shear flow using four different types of titanium dioxide agglomerates in silicone oil, Lee, Feke and Manas-Zloczower (1993) found ke to be proportional to the product FaWa, where Wa is the work of adhesion of the fluid to the particles (nearly equal to the dispersive component of the fluid interfacial tension). Further, increasing the particle porosity sharply increased the erosion rate. This is a consequence of the faster penetration of the fluid into the more porous agglomerates (initially dry), resulting in the reduction of the cohesive strength of the bonds between the primary particles. There is much that remains to be done in this area. For example, erosion of fractal structures does not seem to have been sufficiently studied.
The models for agglomerate rupture when integrated with a flow model are useful for the modeling of dispersion in practical mixers, as was discussed for the case of drop dispersion. Manas-Zloczower, Nir and Tadmor (1982), in an early study, presented a model for the dispersion of carbon black in rubber in a Banbury mixer (Figure 34). The model is based on several simplifying assumptions: Fragmentation is assumed to occur by rupture alone, and each rupture produces two equal sized fragments. Rupture is assumed to occur along a specific plane in the agglomerate (similar to the model of Kendall, 1988) but the strength of the agglomerate is calculated using Rumpf's (1962) model. Hydrodynamic forces are calculated assuming the agglomerate to be a pair of touching spheres (equation (B.1)). The flow in the Banbury mixer is taken to be well-mixed low shear zone from which a stream is continuously passed through a small high shear zone and recycled. Only a fraction of the agglomerates passing through the high shear zone rupture, and this is determined by whether or not the rupture plane is exposed to a sufficiently high force. An agglomerate may break once at most during a single pass through the high shear zone, and no fragmentation takes place in the low shear zone. Statistical arguments are used to obtain the distribution for the number of passes made by an agglomerate through the high shear zone, and to obtain the agglomerate size distribution.
In spite of the simplifying assumptions made in the model, the results give a qualitative insight into the operation of the process. Figure 34 shows the evolution of the agglomerate size distribution with time for a representative case. At the start of the process only large agglomerates (diameter D0) are present; with increasing mixing time the distribution broadens and the peak shifts to smaller sizes. At the same time a new peak is formed corresponding to the aggregate size; aggregates cannot be further ruptured by the flow.
Illustration: Simultaneous erosion and rupture
Agglomerates when sheared at Fa>
Facrit fragment by both rupture and erosion mechanisms.
Experiments of Rwei, Manas-Zloczower and Feke (1992) for carbon black
agglomerates in molten polystyrene show that rupture of the particles occurs
within a short time of application of the shear flow, and a log-normal
distribution of fragment sizes is produced. Subsequent shearing results only in
a slow reduction of the average agglomerate size, and the average radius
decreases exponentially with time ![]() which is characteristic of erosion.
Thus rupture and erosion can be considered to occur sequentially in homogeneous
flows due to their different time scales. However, in flows with spatially
varying shear rates, erosion would occur in all regions of the flow with varying
rates depending on the local value of Fa, while rupture would result during the
first visit of an agglomerate to a high shear zone where Fa > Facrit.
which is characteristic of erosion.
Thus rupture and erosion can be considered to occur sequentially in homogeneous
flows due to their different time scales. However, in flows with spatially
varying shear rates, erosion would occur in all regions of the flow with varying
rates depending on the local value of Fa, while rupture would result during the
first visit of an agglomerate to a high shear zone where Fa > Facrit.
Analysis of the particle size distributions produced in fragmentation processes go back to the early work of Kolmogorov (1941). Considering that the size of fragments produced on breakage are random, Kolmogorov (1941) used statistical arguments, similar to those outlined earlier for the stretching distributions, to show that the size distribution is log-normal. A more general starting point for the study of dispersion of powdered solids is provided by the so-called fragmentation theory (Redner, 1990). Irreversible, continuous breakup of solids in a well-mixed batch system can be described by the linear fragmentation equation,
![]() , (B.16)
, (B.16)
where c(x,t) is the concentration of clusters of mass x at time t, a(x) is the overall rate of breakup of clusters of size x, and f(x|y), the relative rate of breakup, is the expected number of clusters of size x produced from the breakage of a cluster of size y.
The breakup kernels, a(x) and
f(x|y), determine the kinetics of the fragmentation process. However, general
conclusions can be drawn without exact specification of these kernels by scaling
analysis of the fragmentation equations. For example, if small clusters breakup
like larger clusters, behavior experimentally observed in many systems, the
breakage kernels are homogeneous. The overall rate of breakup in this
case is given by ![]() , were l is known as the homogeneity index. Homogeneity
also implies that the distribution of fragments produced on breakup is
, were l is known as the homogeneity index. Homogeneity
also implies that the distribution of fragments produced on breakup is
![]() . (B.17)
. (B.17)
The average number of particles produced
on a single breakup event is then ![]() , and
, and ![]() , due to conservation of mass.
, due to conservation of mass.
The fragmentation equation can be scaled into the following time-invariant form for the case of homogeneous kernels
where both concentration and size are rescaled with respect to the average agglomerate size s(t) as
For conservation of mass it is required that q=2. For the scaled equation (eq. B.18) to be time-invariant, the separation constant (w) given by
must be independent of time. In general, this condition is satisfied at long times as the particle size distribution asymptotically approaches the self-similar distribution, independent of the initial condition.
Filippov (1961) rigorously showed the
above scaling to be valid when l is positive; if l < 0 the scaling
breaks down as mass is lost to the formation of infinitesimal size fragments
(Filippov, 1961). For positive values of l, equation (B.20) gives ![]() at long times.
at long times.
The moments of order a of the bare and scaled size distribution are defined as
![]() , and
, and ![]() . (B.21)
. (B.21)
respectively, and have the form of Mellin
transforms (Morse and Feshbach, 1953). The moments have a physical significance
for the process: for example, M0 is the total number of
clusters per unit volume, and M1 is the total mass per unit
volume. The number average size is then ![]() , and the weight average size
is
, and the weight average size
is ![]() . Finally,
the polydispersity, which characterizes the width of the distribution,
is
. Finally,
the polydispersity, which characterizes the width of the distribution,
is
The scaled moments for the case of homogeneous kernels are obtained as
![]() , with
, with ![]() . (B.23)
. (B.23)
in the limit of long times when the
scaling solution is valid. This recursive relationship between the scaled
moments, and use of inverse Mellin transforms allows the determination the form
of the scaling distribution for the tails of the size distribution (Cheng and
Redner, 1990). In the limit of large mass ![]() , the size distribution is
, the size distribution is
![]() . (B.24)
. (B.24)
The cluster size distribution in the limit
of small mass ![]() depends on the properties of the agglomerates undergoing fragmentation. If
infinitesimal particles are formed on a single breakage, that is
depends on the properties of the agglomerates undergoing fragmentation. If
infinitesimal particles are formed on a single breakage, that is ![]() , then,
, then,
![]() as
as ![]() , (B.25)
, (B.25)
and if clusters are broken into small fragments by several steps, then the distribution is log-normal in the limit of small x. This is in agreement with the theory of Kolmogorov (1941). Thus, limiting forms of the cluster size distribution are obtained by invoking only the assumption of homogeneous breakup kernels.
Several works, over the last decade or so, (Ziff, 1991; Ziff and McGrady, 1986; McGrady and Ziff, 1987, 1988; and Williams, 1990) have addressed the behavior of systems with specified breakup kernels. Certain specific forms for the breakup kernels lead to analytical solutions for the cluster size distribution. For example, Ziff (1991) obtained explicit forms of the size distribution for homogeneous breakup kernels of the form
![]() (B.26)
(B.26)
where q, a and b are adjustable parameters, which allow for fitting of a range of breakup processes. The limiting forms of these solutions are predicted by the preceding analysis.
Erosion-controlled fragmentation
The dynamics of the particle size distribution produced by fragmentation processes dominated by erosion are qualitatively different from those involving rupture. While the rate of breakage function is homogeneous (a(x)=kxl) since the rate of erosion is proportional to surface area, the distribution of fragments produced on breakage, in general, is not homogeneous. As seen earlier, erosion produces small fragments with a relatively narrow Gaussian distribution. Thus, each erosion step may be considered as a binary breakup process forming one fragment of size e and one of size y-e, with y>>e. With these assumptions the relative rate of breakup becomes
![]() , (B.27)
, (B.27)
where y is the mass of the parent agglomerate and e is the mass of primary particle (aggregate).
A solution to this problem (Hansen and Ottino, 1996a) reveals that the cluster size distribution is bimodal, as expected, with c(x,t) for large-x dependent upon the initial conditions (Figure 35a). The distribution thus does not approach a self-similar form and the scaling results above are not valid for this problem. This is a result of the non-homogeneous relative rate of breakup.
Experimental data of erosion processes are limited -- but there is some data from the comparable process of attrition. Neil and Bridgwater (1994) determine, by sieving, the cumulative mass fraction of clusters M(l), with a characteristic length less than l. Hansen and Ottino (1996a) assume that x?prl3/6, where r is the density of the solids. Figure 35b shows the fitting to available experimental data. Deviation of the experimental data from the model could be due to inefficiencies in the sieving process, the assumed relationship between x and l, and/or the presence of rupture. Better data are clearly needed before hard conclusions can be drawn (concentrations would be more enlightening than cumulative mass, and the reported size distributions are relatively narrow). It is nevertheless apparent that the relative constancy of M(l) with l indicates the presence of a bimodal distribution.
Advection is important in fragmentation processes, and an initially homogeneous system may evolve spatial variations due to spatially dependent fragmentation rates. For example, Figure 36 shows the spatial distribution of eroded clusters in the journal bearing flow operating under good mixing and poor mixing conditions (Hansen, 1997). Clusters are eroded by hydrodynamic stresses and parent clusters are color coded in the Figure according to size. The aggregates eroded from the cluster are not shown. The poorly mixed system (Figure 36a) clearly shows large clusters (clusters eroded to a lesser extent) trapped in a regular island in which the shear rates are low, and small clusters near the inner cylinder where the shear rates are high. However, even the well mixed system shows spatial variations of cluster sizes, indicating that the rate of mixing is not fast enough to eliminate the fluctuations produced by the spatially dependent fragmentation rate. Such spatial variations would undoubtedly cause deviations from predictions of mean field theories for the cluster size distribution.
Consider now continuous irreversible breakup by both rupture and erosion mechanisms in a well-mixed system. As in the model of erosion discussed above, we assume that clusters consist of particles of mass e, and that e<<s(t), so that the discrete size distribution may be approximated as a continuum. The fragmentation equation for simultaneous rupture and erosion for the case of homogeneous rupture kernels is (Hansen and Ottino, 1996a)
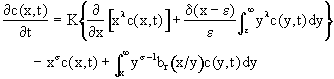 , (B.28)
, (B.28)
where l and s are the homogeneity indices for erosion and rupture, respectively. The first term on the right hand side accounts for erosion, and the next two terms account for rupture.
A characteristic parameter of the process is the ratio of the overall rate of erosion relative to the overall rate of rupture given by
![]() . (B.29)
. (B.29)
This ratio determines the applicability of
the scaling solution: if ![]() , the scaling solution breaks down as s(t) approaches zero.
, the scaling solution breaks down as s(t) approaches zero.
Consider next the case of binary rupture
when ![]() , s=1
and
, s=1
and ![]() . Assuming
that fragments once eroded do not fragment further, an approximate form of the
evolution equation for clusters larger than size e is
. Assuming
that fragments once eroded do not fragment further, an approximate form of the
evolution equation for clusters larger than size e is
![]() . (B.30)
. (B.30)
The mass of the eroded fragments can then be obtained from the mass balance. The solution breaks down as the average size (s) approaches the aggregate size (e). Following Ziff and McGrady (1985), particle size distribution is obtained as
![]() (B.31)
(B.31)
for the initial condition ![]() . Since the kinetic
equation (eq. B.30) is linear, the solutions for other initial conditions are
easily obtained by superposition.
. Since the kinetic
equation (eq. B.30) is linear, the solutions for other initial conditions are
easily obtained by superposition.
- Rate of erosion is directly proportional to the fragmentation number and the surface area of the parent agglomerate.
- Bimodal cluster size distribution.
- Model computations indicate that for short-times, polydispersity is inversely proportional to average size.
- Size distribution is not self-similar.
- Size distributions of fragments produced in a single rupture event are self-similar.
- For fractal agglomerates, the critical
fragmentation number is inversely proportional to its volume ![]() .
.
- Homogeneous breakage kernels with positive homogeneity index (l>0) produce self-similar size distributions at long times.
Aggregation of particles may occur, in general, due to Brownian motion, buoyancy induced motion (creaming) and relative motion between particles due to an applied flow. Flow-induced aggregation dominates in polymer processing applications because of the high viscosities of polymer melts. Controlled studies -- the conterpart of the fragmentaion studies described in the previous section -- may be carried in simple flows, such as in the shear field produced in a cone and plate device (Chmimili 1996). The number of such studies appears to be small.
At the simplest level, the rate of flow induced aggregation of compact spherical particles is described by Smoluchowski's theory (equation (A.22)). Such expressions may then be incorporated into population balance equations to determine the evolution of the agglomerate size distribution with time. However, with increase in agglomerate size, complex (fractal) structures may be generated which preclude analysis by simple methods as above.
Let us illustrate first how different (idealized) aggregation processes may result in different structures. There is extensive literature on diffusion limited aggregation (DLA) (for a comprehensive review see Meakin 1988). Three methods of simulation are common: (standard) diffusion limited aggregation (DLA), reaction limited aggregation (RLA) and linear trajectory aggregation (LTA). DLA structures are generated by placing a seed particle in the middle of a lattice. Other particles are placed in the lattice and follow a random walk trajectory. These moving particles bind onto the growing seed upon contact to form a cluster. In general, clusters produced by DLA simulations are fractal, and the fractal dimension of the clusters is approximately 2.5 (Figure 37). The difference between RLA and DLA is that a sticking probability governs the binding in RLA. Thus, particles penetrate further into the growing agglomerate, and denser agglomerates are formed. The dimension of RLA clusters is greater than 2.5 and increases with a decreasing sticking probability. LTA is similar to DLA, with particles following a random linear trajectory instead of a random walk. LTA, which models agglomerates formed by mechanical motion such as a mixing processes, yields compact structures with a fractal dimension close to 3.
Unlike the simulations which only consider particle-cluster interactions discussed earlier, hierarchical cluster-cluster aggregation (HCCA) allows for the formation of clusters from two clusters of the same size. Clusters formed by this method are not as dense as clusters formed by particle-cluster simulations, because a cluster cannot penetrate into another cluster as far as a single particle can (Figure 37). The fractal dimension of HCCA clusters varies from 2.0 to 2.3 depending on the model used to generate the structure: DLA, RLA, or LTA. For additional details, the reader may consult Meakin (1988).
The direct relevance of these diffusion-driven aggregation models to flow-driven aggregation is somewhat questionable, though they serve to highlight the influence of the aggregation process on the structures produced. These models have been used to synthesize structures to investigate how they break (Horwatt et al., 1992a,b).
Flow induced aggregation may also result in the formation of agglomerates with complex (fractal) structure (Jiang and Logan 1996). An understanding of the structures formed in the aggregation process is important -- the kinetics of the aggregation is significantly affected by the type of structures formed as we will see in the following sections. The kinetics in turn affect the evolution of the agglomerate size distribution, which is the quantity of primary interest from a practical viewpoint.
GLOBAL SCALES: AGGLOMERATE SIZE DISTRIBUTIONS
Analytical approaches to obtain the agglomerate size distribution are possible for well-mixed systems and when the rate of aggregation of clusters is defined by simple functions. In general, irreversible aggregation in well-mixed systems is described by Smoluchowski's coagulation equation, which for a continuous distribution of cluster sizes can be written as
![]() , (B.32)
, (B.32)
where c(x,t) is the concentration of clusters of mass x at time t and K(x,y) is the rate of aggregation of clusters of masses x and y (van Dongen and Ernst, 1988)). The first term on the right hand side accounts for the formation of a cluster of size x due to aggregation of two clusters of size x-y and y, whereas the second term represents the loss of clusters of mass x. There are significant parallels between this equation and the fragmentation equation.
Scaling solutions, as in the case of fragmentation, are possible if the kernel K(x,y) is homogeneous, which requires that
![]() , (B.33)
, (B.33)
where k is the homogeneity index. The above condition is not very restrictive; for example, the aggregation rate given by Smoluchowski's theory (equation A.22) is homogeneous with k=1. Time-invariant scaled solutions are obtained in this case if the concentration is scaled as
![]() . (B.34)
. (B.34)
where h = x/s(t) and s(t) is the average size, as before The relationship between the scaled concentration for fragmentation (f) and y is then
![]() . (B.35)
. (B.35)
This scaling (or self-similarity) is verified by numerous computational and theoretical studies (for a review see Meakin (1992)).
For many well studied rate of aggregation
kernels, the average cluster size grows algebraically, s(t)~tz. In fact, when K(x,y) is homogeneous and k, as defined in equation
(B.35), is less than unity, we get ![]() . When
. When ![]() loss of mass to the formation of
infinite size clusters -- the opposite of shattering in fragmentation, termed
gelling -- occurs in finite time.
loss of mass to the formation of
infinite size clusters -- the opposite of shattering in fragmentation, termed
gelling -- occurs in finite time.
Smoluchowski's equation, like the
fragmentation equation can be written in terms of the scaling distribution.
Furthermore, general forms may be determined for the tails of the scaling
distribution-- limits of small mass, ![]() , and large mass,
, and large mass, ![]() . The details can be found in van
Dongen and Ernst (1988).
. The details can be found in van
Dongen and Ernst (1988).
If the scaling form given above holds, then the bare and scaled moments are related by
![]() (B.36)
(B.36)
Hence, the polydispersity (eq. B.22) is
independent of time, provided ![]() is bounded. Moreover, if
is bounded. Moreover, if ![]() , as is expected for a rate
of aggregation independent of mass (Schumann, 1940), the polydispersity is equal
to 2. Also note that
, as is expected for a rate
of aggregation independent of mass (Schumann, 1940), the polydispersity is equal
to 2. Also note that
![]() , (B.37)
, (B.37)
and therefore number average and weight average sizes are proportional to each other when scaling used for the fragmentation equation is applicable and the integral of f(h) is bounded.
Consider the initial evolution of the size distribution of an aggregation process for small deviations from monodisperse initial conditions. Assume, as well, that the system is well-mixed so that spatial inhomogeneities may be ignored. Of particular interest is the growth rate of the average cluster size and how the polydispersity scales with the average cluster size.
This can be done by developing equations for the moments-- for example multiplying Smoluchowski's equation by xadx, integrating from 0 to infinity, and manipulating the limits of integration yields (Hansen and Ottino, 1996b)
![]() . (B.38)
. (B.38)
Expand the new kernel,
![]() ., (B.39)
., (B.39)
in a series about the average cluster size yields
![]() , (B.40)
, (B.40)
where ![]() denotes
denotes ![]() evaluated at x=1 and y=1 (this
assumes that most of the clusters are relatively close to the average cluster
size, i.e., the polydispersity is close to unity). Considering the number
average cluster size
evaluated at x=1 and y=1 (this
assumes that most of the clusters are relatively close to the average cluster
size, i.e., the polydispersity is close to unity). Considering the number
average cluster size ![]() , we determine that
, we determine that
![]() . (B.41)
. (B.41)
which can be rewritten in terms of the moments as
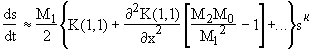 , (B.42)
, (B.42)
where the higher order terms include combinations of larger moments which are small when the polydispersity is near unity. Hence, when the polydispersity is close to unity the average cluster size is described by
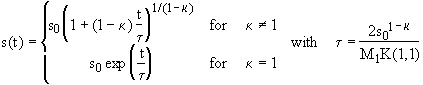 . (B.43)
. (B.43)
Here s0 denotes the initial average cluster size.
Similar arguments can be used to determine the behavior of the zeroth and second moments. For example, the polydispersity evolves according to
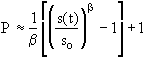 where
where ![]() , (B.44)
, (B.44)
for polydispersities near unity.
It should be noted that the predictions for the number average cluster size and polydispersity, agree with analytical results for K(x,y)=1, x+y, and xy. Furthermore, the short-time form of number average size in equation (B.43) matches the form of s(t) predicted by the scaling ansatz. Computational simulations (Hansen and Ottino, 1996b) also verify these predictions (Figure 38).
In this section, we consider flow induced aggregation without diffusion, i.e., the Péclet number, PeºVL/D, where V and L are the characteristic velocity and length and D is the Brownian diffusion coefficient, is much greater than unity. For simplicity, we neglect the hydrodynamic interactions of the clusters, and highlight the effects of advection on the evolution of the cluster size distribution and the formation of fractal structures.
Torres, Russel and Schowalter (1991a,b) have examined structure formation due to aggregation driven by shear and elongational flows. Two cases were computationally examined: particle-cluster aggregation, and cluster-cluster aggregation. In the case of particle-cluster aggregation, a particle is placed at a random position relative to the cluster and is advected by the flow. Rapid coagulation is assumed so that the particle aggregates with the cluster upon collision. The cluster-cluster aggregation procedure is similar but with the particle replaced by a cluster of the same size as the site cluster. Clusters formed in particle-cluster simulations are denser than suggested by experiments Torres et al. (1991a). On the other hand, the cluster-cluster simulations agree with experiments in shear flows carried out by the same investigators, suggesting the formation of clusters is dominated by cluster-cluster aggregation. The fractal dimension of the aggregates formed in both shear and elongational flows by the cluster-cluster simulations is about 1.8 Torres et al. (1991b).
Only a few studies have considered aggregation in complex flows, in particular chaotic flows. Unlike studies of aggregation by kinetic equations, these simulations allow for spatial variations. A computational study (Muzzio and Ottino 1988), focusing on compact clusters in a 2D chaotic flow (blinking vortex flow), shows that islands of regularity may cause spatial variations in the rate of aggregation, and that aggregation in "well-mixed" chaotic systems is similar mathematically to Brownian aggregation and can be described by Smoluchowski's equation. The effect of mixing on the fractal nature of clusters is considered explicitly by Danielson et al. (1991). They determined that the fractal dimension can be controlled by varying the degree of mixing in chaotic flows. The variation of fractal dimension with mixing is due to the nature of interactions of monomers and larger clusters in different mixing schemes. If the system is not well-mixed (large islands), the large clusters, which are trapped in islands, do not interact with each other and the process resembles the particle-cluster aggregation of Torres et al. (1991b). However, if the system is well-mixed (no islands), then larger clusters interact with each other and aggregation resembles cluster-cluster aggregation. Thus, the fractal dimension of a cluster is expected to decrease with better mixing.
We focus on aggregation in model regular and chaotic flows. Two aggregation scenarios are considered: in (i) the clusters retain a compact geometry -- forming disks and spheres-- whereas in (ii) fractal structures are formed. The primary focus of (i) is kinetics and self-similarity of size distributions, while the main focus of (ii) is the fractal structure of the clusters and its dependence with the flow.
Here we consider aggregation in a physically realizable chaotic flow, the journal bearing flow or the vortex mixing flow described earlier. The computations mimic fast coagulation; particles seeded in the flow are convected passively and aggregate upon contact. In this example the clusters retain a spherical structure and the capture radius is independent of the cluster size.
The evolution of the average cluster size
is shown in Figure 39a. In a well-mixed system the growth of the average cluster
size is linear with time (Hansen and Ottino, 1996b). In a poorly-mixed system, a
system with small chaotic regions, the average cluster size grows less
fast ![]() , with a
small variation in the exponent with the capture radius of the clusters. The
growth of the average cluster in a regular flow, i.e., no chaos present, is
included for completeness. Intuitively, one may expect the aggregation in the
poorly-mixed system to be a hybrid of aggregation in the well-mixed flow and in
the regular flow, but this is not the case. Surprisingly, the growth rate of the
average cluster in the regular flow, approaching linear growth, is faster than
in the poorly-mixed flow.
, with a
small variation in the exponent with the capture radius of the clusters. The
growth of the average cluster in a regular flow, i.e., no chaos present, is
included for completeness. Intuitively, one may expect the aggregation in the
poorly-mixed system to be a hybrid of aggregation in the well-mixed flow and in
the regular flow, but this is not the case. Surprisingly, the growth rate of the
average cluster in the regular flow, approaching linear growth, is faster than
in the poorly-mixed flow.
As previously discussed, we expect the scaling to hold if the polydispersity, P, remains constant with respect to time. For the well-mixed system the polydispersity reaches about two when the average cluster size is approximately ten particles, and statistically fluctuates about two until the mean field approximation and the scaling break down, when the number of clusters remaining in the system is about 100 or so. The polydispersity of the size distribution in the poorly-mixed system never reaches a steady value. The ratio M3M1/M22, which is constant if the scaling holds and mass is conserved, is also unsteady in the poorly-mixed flow, indicating that the cluster size distribution is not self-similar in poorly-mixed flows. The polydispersities of the clusters in the poorly-mixed and well-mixed flows are compared in Figure 39b. The polydispersity of clusters in a regular flow, also included in Figure 39b, initially increases then slowly approaches unity as the number of clusters approaches one. The higher polydispersity for clusters formed in the poorly-mixed flow is indicative of the wider range of cluster sizes present in the system.
The self-similar nature of the cluster size distributions for the well-mixed flow is shown in Figure 39c. Due to the discrete nature of cluster size in the simulations, this figure shows the cumulative mass fraction, as it is less prone to statistical fluctuations (a scaled cluster size distribution is also included for clarity). It should be noted that the cumulative size distribution scales as
![]() . (B.45)
. (B.45)
Thus, we plot M(x,t)/M1 versus x/s(t). As noted earlier, the cluster size distribution and the first moment of the size distribution are averaged over the entire journal bearing. As indicated by the behavior of P in Figure 39b, the cluster size distribution becomes self-similar when the average size is about ten particles per cluster.
Illustration: Aggregation of area-conserving clusters in two dimensional chaotic flows
Particles, convected passively in a two dimensional chaotic flow, aggregate on contact to form clusters. The capture radius of the clusters increases with the size of the cluster. Since these simulations are in two dimensions, the area of the aggregating clusters is conserved.
The rate of aggregation of clusters with the same capture radius in two dimensions is proportional to the area of the cluster (Muzzio and Ottino, 1988). If this dependence of the rate of aggregation on cluster size holds for clusters with different capture radii, then the aggregation in these simulations is on the verge of gelation (van Dongen and Ernst, 1988). Simulations show that for aggregation of area-conserving clusters the formation of one large cluster predominates, but an infinite cluster is not formed since the system is finite. This large cluster is formed before the scaling distribution is reached.
In a system with a small chaotic region, the rate of aggregation in the regular region is significantly slower than in the chaotic region. Thus, the polydispersity of the clusters remains large until the regular region is "broken" by the increasing capture radius of the cluster. However, the regular region retains its identity if the capture radius of the clusters does not become large enough so that clusters in the regular region aggregate with clusters in the chaotic region.
As shown in Figure 40, the average cluster
size in a well-mixed or chaotic system evolves as ![]() . There are small variations in the
exponent with the area fraction of the clusters. The growth rate of the average
cluster size in a poorly-mixed system follow the same form; however, the
exponent is quite different. In a poorly-mixed system, the exponent is dependent
upon the area fraction of clusters. For one flow studied, when the area fraction
of clusters is 0.02 the exponent is 0.81. When the area fraction of clusters is
increased to 0.1 the rate of aggregation increases dramatically-- the exponent
is 25. In fact, it is difficult to determine if this high rate of aggregation is
algebraic or exponential. This implies that above some critical area fraction of
clusters the large clusters are more likely to aggregate, while small clusters
are more likely to aggregate below some critical area fraction of clusters. In
the poorly-mixed system, it appears that the growth rate changes as aggregation
proceeds because clusters in the chaotic region become large enough to aggregate
with clusters in the regular region.
. There are small variations in the
exponent with the area fraction of the clusters. The growth rate of the average
cluster size in a poorly-mixed system follow the same form; however, the
exponent is quite different. In a poorly-mixed system, the exponent is dependent
upon the area fraction of clusters. For one flow studied, when the area fraction
of clusters is 0.02 the exponent is 0.81. When the area fraction of clusters is
increased to 0.1 the rate of aggregation increases dramatically-- the exponent
is 25. In fact, it is difficult to determine if this high rate of aggregation is
algebraic or exponential. This implies that above some critical area fraction of
clusters the large clusters are more likely to aggregate, while small clusters
are more likely to aggregate below some critical area fraction of clusters. In
the poorly-mixed system, it appears that the growth rate changes as aggregation
proceeds because clusters in the chaotic region become large enough to aggregate
with clusters in the regular region.
Illustration: Aggregation of fractal structures in chaotic flows
In a further study of aggregation in two dimensional chaotic flows, the passively convected clusters retain their geometry after aggregation, i.e., fractal structures are formed. A typical fractal cluster resulting from these simulations is shown in Figure 41.
The kinetics of fractal structures differ
significantly from the kinetics of compact structures. As with the
area-conserving compact structures, no self-similar distribution is observed.
However, fractal clusters grow faster than compact structures. This is
highlighted in Figure 40 which illustrates that the average cluster size of
fractal structures grows nearly exponentially, while the average cluster size of
compact structures grows algebraically. The growth of fractal structures in the
poorly-mixed system is accurately described by ![]() ; however, aggregation in the
well-mixed system may only be approximated by the exponential form.
Interestingly, the overall rate of aggregation of fractal structures is first
order, while the overall rate of aggregation of clusters with a constant capture
radius is second order in the well-mixed system. The rate of aggregation of
area-conserving clusters fits between first order and second order.
; however, aggregation in the
well-mixed system may only be approximated by the exponential form.
Interestingly, the overall rate of aggregation of fractal structures is first
order, while the overall rate of aggregation of clusters with a constant capture
radius is second order in the well-mixed system. The rate of aggregation of
area-conserving clusters fits between first order and second order.
Note that only one system, the one corresponding to constant capture radius clusters in chaotic flows, behaves as expected via mean field predictions. In general, the average cluster size grows fastest in the well-mixed system. However, in some cases the average cluster size in the regular flow grows faster than in the poorly-mixed system.
Furthermore, since the average cluster
size of fractal clusters grows exponentially, we do not expect the scaling to
hold. The argument is that k would be unity if the scaling ansatz were
applicable here, but that the scaling is not valid for ![]() and therefore not applicable to this
case. Indeed, the polydispersity does not approach a constant value, indicating
that the scaling does not apply. Again, significant differences between the
polydispersities of fractal structures and compact structures are shown in
Figure 38. Initially, P increases rapidly, as is shown in Figure 38 the
polydispersity of fractal clusters grows faster than the polydispersity of their
compact counter-parts. Furthermore, in these simulations, P of fractal
structures approaches unity sooner.
and therefore not applicable to this
case. Indeed, the polydispersity does not approach a constant value, indicating
that the scaling does not apply. Again, significant differences between the
polydispersities of fractal structures and compact structures are shown in
Figure 38. Initially, P increases rapidly, as is shown in Figure 38 the
polydispersity of fractal clusters grows faster than the polydispersity of their
compact counter-parts. Furthermore, in these simulations, P of fractal
structures approaches unity sooner.
The long-time behavior of the polydispersity suggests that only one system, the well-mixed system with constant capture radius, may be described by the scaling ansatz. The scaling breaks down in poorly-mixed systems due to spatial fluctuations. In other systems, aggregation of area-conserving or fractal clusters, the scaling breaks down because aggregation is dominated by formation of one or several large clusters.
The fractal nature of the structures is also of interest. Due to the wide range of flow in the journal bearing, a distribution of fractal clusters is produced. When the area fraction of clusters is 0.02, the median fractal dimension of the clusters is dependent on the flow, similar to the study by Danielson et al. (1991). The median fractal dimension of clusters formed in the well-mixed system is 1.47 while the median fractal dimension of clusters formed in the poorly-mixed case is 1.55. Furthermore, the range of fractal dimensions is higher in the well-mixed case.
The results are different when the area fraction of clusters increases. The distribution of the fractal dimension of the clusters for a system with an area fraction of clusters of 0.10 is shown in Figure 42. The median fractal dimension of the clusters is independent of the flow and is approximately 1.47. Since the fractal dimension of the clusters is closer to the dimension of the clusters in the well-mixed system with a lower area fraction of clusters, this suggests that as the area fraction of clusters increases, the island of regularity gets broken up by the increasing capture radius of the clusters. Thus, aggregation in the poorly-mixed system behaves similarly to that in the well-mixed system when aggregation occurs between the two disjoint regions of the flow.
* Fractal dimension of clusters formed by flow induced aggregation is independent of local flow type.
* Fractal dimension depends on mixing in chaotic flows: good mixing (no islands) gives lower fractal dimensions.
* Model computations indicate that the average cluster size:
- grows exponentially for fractal structures.
- has the fastest rate of growth in well-mixed systems.
- for long times is
(i) constant~2 for constant capture radius clusters in a well-mixed system.
(ii) non-constant for poorly-mixed systems, and for area-conserving compact and fractal clusters.
The modeling of mixing processes has undergone exciting progress in the last few years. Computations have reached maturity and exploitation of concepts and results in the context of realistic devices is now a reality (Avalosse and Crochet, 1997a,b). But much, if not all, of the advances have been restricted to single phase fluids. One would expect that similar advances will take place in dispersion of solids and liquids in viscous flows. One may also speculate as to whether modeling or theory will drive experiments or the other way around. One might argue that as things are now, theory is ahead and that more experiments are badly needed. But the theory picture, described at length in the previous sections, is clearly incomplete and one may argue that more realism is needed.
As pointed out earlier most of the examples involve "one-sided" interactions: the microstructures are acted on by the chaotic flow but they do not modify the flow structure itself. Not much has been done regarding these interactions in the context of chaos and mixing and it is probably useful to point out here whatever little is known. An example of coupling involves dilute viscoelastic fluids (polymer solutions) in chaotic flows. A general finding is the rate of mixing seems always to be slowed down by elasticity. A second general example along the lines of microstructures and flow is the presence of a dispersed phase which alters the flow patterns, and computational studies have shown how regular islands can be broken as a consequence. Little is known, in general, in this case as well.
The caveats notwithstanding practical applications based on already existing theory seem possible. Zumbrunen et al. have studied experimentally the possibility of developing fine scale structures of dispersed phased by exploiting chaotic three-dimensional flows (Liu and Zumbrunnen 1996, Zumbrunnen, Miles, and Liu 1996) and Liu and Zumbrunnen (1997) note that significant improvements in impact properties of a polystyrene matrix can be achieved by adding small volume fraction (~9%) of low density polyethylene. As opposed to conventional dispersion methods, where the minor phase may consist of randomly distributed small droplets, controlled chaotic mixing produces highly connected stretched and folded structures which can be preserved upon solidification.
The interaction between the dispersed phase elements at high volume fractions has an impact on breakup and aggregation, which is not well understood. For example, Elemans et al. (1997) found that when closely spaced stationary threads break by the growth of capillary instabilities, the disturbances on adjacent threads are half a wavelength out of phase (Figure 43), and the rate of growth of the instability is smaller. Such interaction effects may have practical applications, for example, in the formation of monodisperse emulsions (Mason and Bibette, 1996).
While the fundamentals of breakup of drops are reasonably well-understood, the physics of the fragmentation of clusters is not as well grounded. Characterization of the structure and the measurement of the strength of agglomerates need to be addressed in greater detail. However, as in the case of liquid-liquid dispersions, existing concepts provide inspiration for possible new technologies, as suggested, for example, by Danescu and Zumbrunnen (1997) for the case of conductive composites involving small volume fraction of a conductive component. Both extremes, no-mixing and "perfect" mixing, lead to poor overall conductivities. No-mixing corresponds to the case a large isolated agglomerates in a polymer matrix; "perfect" mixing, to randomly placed aggregates have little contact with each other. At low volume fractions there are no sample-spanning clusters percolating through the sample and the conductivity is poor. The best conductivities result when the particles are still recognizable as being aligned in long thin interconnected structures, before further mixing randomizes the particles and connectivity is lost. There has been, for some time, industrial empirical evidence that "too much mixing" may not be good, and in this case, existing theory provides a rationalization of the observed events.
Integrating the fundamental processes at drop/cluster length scales to realistic flow fields is another area which is still developing and the gap between the work presented here and more practical extrusion applications (Rauwendaal 1994, White 1990) needs to be bridged. Advances in this field would undoubtedly have an impact on the analysis and design of mixing equipment, as well as for optimization of processing conditions for mixers. All these issues require in-depth study before applications emerge.
Its should be stressed again that the
application of the concepts presented here is relevant to polymer and rubber
procesing and composite applications -- which form now a fertile ground for the
application of these ideas -- as well to a variety of consumer products
industries where product value is intimately tied up to the creation of unique
structures. Examples in this area may range from food products, such as ice
cream and margarine, to laundry and personal care products such as dishwasher
liquids, creams, and lotions. The creation of an organized body of knowledge
geared towards the consumer product area presents considerable opportunities
(Villadsen 1997).
Acknowledgment: The research presented here has been supported over the last decade or so by grants to JMO awarded by the National Science Foundation, the Department of Energy - Basic Energy Sciences and 3M.
Acrivos, A. (1983) The breakup of small drops and bubbles in shear flows, 4th International Conference on Physicochemical hydrodynamics, Ann. N. Y. Acad. Sci., 404, 1-11.
Aref, H. (1984) Stirring by chaotic advection, J. Fluid Mech., 143, 1-21.
Alder, P. M. and Mills, P. M. (1979) Motion and rupture of a porous sphere in a linear flow field, J. Rheol. 23, 25-37.
Austin, L. G. (1971) A review introduction to the mathematical description of grinding as a rate process, Powder Technol. 5, 1-17.
Avalosse, Th. (1993) Simulation numerique du melange laminaire par elements finis, Ph.D. Thesis, Université Catholique de Louvain, Belgium.
Avalosse, Th. and Crochet, M.J., (1997a) Finite element simulation of mixing: 1. Two-dimensional flow in periodic geometry, AIChE J., 43, 577-587.
Avalosse, Th. and Crochet, M.J., (1997b) Finite element simulation of mixing: 2. Three-dimensional flow through a Kenics mixer, AIChE J., 43, 588-597.
Bagster, D. F. and Tomi, D. (1974) The stresses within a sphere in simple flow fields, Chem. Eng. Sci. 29, 1773-1783.
Barthès-Biesel, D., and Acrivos, A. (1973) deformation and burst of a liquid droplet freely suspended in a linear shear field, J. Fluid Mech., 61, 1-21.
Batchelor, G. K. and Green, J. T. (1972) The hydrodynamic interaction of two small freely-moving spheres in a linear flow field, J. Fluid Mech. 56, 375-400.
Becher, P. and McCann, M. (1991) The process of emulsification: A computer model, Langmuir, 7, 1325-1331.
Bentley, B.J. and Leal, L.G. (1986) a computer-controlled four-roll mill for investigations of particle and drop dynamics in two-dimensional linear shear flows, J. Fluid Mech., 167, 219-240.
Bidkar, U. R. and Khakhar, D. V. (1990) Collision rates in chaotic flows: Dilute suspensions, Phys. Rev. A 42, 5964-5969.
Bigg, D. and Middleman, S. (1974) laminar mixing of a pair of fluids in a rectangular cavity, Ind. Eng. Chem. Fundam., 13, 184-190.
Brenner, H. (1958) Dissipation of energy due to solid particles suspended in a viscous liquid, Phys. Fluids, 1, 338-346.
Brunk, B.K., Koch, D.L., and Lion, L.W. (1997) Hydrodynamic pair diffusion in isotropic random velocity fields with application to turbulent coagulation, Phys. Fluids, 9, 2670-2691
Chakravarthy, V.S. and Ottino, J.M. (1996) mixing of two viscous fluids in a rectangular cavity, Chem. Eng. Sci., 51, 3613-3622.
Chella, R. and Ottino, J.M. (1985) Fluid mechanics of mixing in a single-screw extruder, I&EC Fundamentals, 24, 2, 170-180.
Chella, R. and Viñals, J. (1996) Mixing of a two phase fluid by cavity flow, Phys. Rev. E, 53, 3832-3840.
Cheng, Z. and Redner, S. (1990) Kinetics of fragmentation, J. Phys. A: Math. Gen. 23, 1233-1258.
Chesters, A.K. (1991) The modeling of coalescence processes in fluid-liquid dispersions: A review of current understanding, Trans. Inst. Engrs., 69, 259-270.
Chimmili, S. (1996) Shear induced agglomeration in particulate suspensions, M.Sci. thesis, West Virginia University.
Danescu, R.I., Zumbrunnen, D.A. (1997) Creation of conducting networks of particles in polymer melts by chaotic mixing, J. Thermoplastic Comp. Materials, submitted.
Danielson, T. J., Muzzio, F. J. and Ottino, J. M. (1991) Aggregation and structure formation in chaotic and regular flows, Phys. Rev. Lett. 66, 3128-3131.
de Bruijn, R.A. (1993) Tipstreaming of drops in simple shear flows, Chem. Eng. Sci., 48, 2, 277-284.
DeRoussel, P. (1997) Mixing and dispersion of viscous liquids, Ph.D. Thesis in progress, Northwestern University, U.S.A.
Eggers, J. (1997) Nonlinear dynamics and breakup of free surface flows, Rev. Modern Phys., in press.
Elemans, P.H.M., van Wunnik, J.M., and van Dam, R.A. (1997) Development of morphology in blends of immiscible polymers, AIChE J., 43, 1649-1651.
Erwin, L. (1978) Theory of mixing sections in single screw extruders, Polym. Eng. Sci., 18, 7, 572-576.
Feke, D. L. and Manas-Zloczower, I. (1991) Rupture of inhomogeneous spherical clusters by simple flows, Chem. Eng. Sci. 46, 2153-2156.
Filippov, A. F. (1961) On the distribution of the sizes of particles which undergo splitting, Theory of Probab. and its Appl. (Engl. Transl.) 4, 275-294.
Franjione, J.G. and Ottino, J.M. (1987) Feasibility of numerical tracking of material lines and surfaces in chaotic flows, Phys. Fluids, 30, 3641-3643.
Giesekus, H. (1962) Strömungen mit konstantem Geschwindigkeitsgradienten und die Bewegung von darin suspendierten Teilchen, Rheol. Acta, 2, 112-122.
Grace, H.P., Dispersion phenomena in high viscosity immiscible fluid systems and application of static mixers as dispersion devices in such systems, 3rd Eng. Found. Conf. Mixing, Andover, N.H., Republished 1982 in Chem. Eng Commun., 14, 225-227.
Hansen, S. and Ottino, J. M. (1996a) Agglomerate erosion: A nonscaling solution to the fragmentation equation, Phys. Rev. E 53, 4209-4212.
Hansen, S. and Ottino, J. M. (1996b) Aggregation and cluster size evolution in nonhomogeneous flows, J. Colloid Interface Sci. 179, 89-103.
Hansen, S. (1997) Aggregation and fragmentation in chaotic flows of viscous fluids, Ph.D. Thesis, Northwestern University, U.S.A.
Hartley, P.A. and Parfitt, G.D. (1984) An improved split cell apparatus for the measurement of tensile strength of powders, J. Phys. E, Sci. Instrum., 17, 347- 349.
Hobbs, D.M. and Muzzio, F.J. (1997), "The Kenics static mixer: a three-dimensional chaotic flow," Chem. Eng. J., 67, 3, 133-166.
Horwatt, S. W., Feke, D. L. and Manas-Zloczower, I. (1992a) The influence of structural heterogeneities on the cohesivity and breakup of agglomerates in simple shear flow, Powder Technol. 72, 113-119.
Horwatt, S. W., Manas-Zloczower, I. and Feke, D. L. (1992b) Dispersion behavior of heterogeneous agglomerates at supercritical stresses, Chem. Eng. Sci. 47, 1849-1855.
Huneault, M.A., Shi, Z.H., and Utracki, L.A. (1995) Development of polymer blend morphology during compounding in a twin-screw extruder. Part IV: A new computational model with coalescence, Polym. Eng. Sci., 35, 1, 115-127.
Jana, S.C., Metcalfe, G. and Ottino, J.M. (1994) Experimental and computational studies of mixing in complex Stokes flow - the vortex mixing flow and the multicellular cavity flow, J. Fluid Mech., 269, 199-246.
Jana, S.C., Tjahjadi, M. and Ottino, J.M. (1994) Chaotic mixing of viscous fluids by periodic changes in geometry - baffled cavity flow, AIChE J., 40, 1769-1781.
Janssen, J.M.H. (1993) Dynamics of Liquid-Liquid Mixing, Ph.D. Thesis, Eindhoven University of Technology.
Janssen, J.M.H. and Meijer, H.E.H. (1993) Droplet breakup mechanisms: stepwise equilibrium versus transient dispersion, J. Rheol., 37, 4, 597-608.
Janssen, J.M.H. and Meijer, H.E.H. (1995) Dynamics of liquid-liquid mixing: A 2-zone mixing model, Polym. Eng. Sci., 35, 22, 1766-1780.
Jiang, Q. and Logan, B.E. (1996) Fractal dimensions of aggregates from shear devices, J. AWWA, February, pp. 100-113.
Kaper, T.J. and Wiggins, S. (1993) An analytical study of transport in Stokes flows exhibiting large scale chaos in the eccentric journal bearing, J. Fluid Mech., 253, 211-243.
Kao, S.V. and Mason, S.G. (1975) Dispersion of particles by shear, Nature 253, 619-621.
Kendall, K. (1988) Agglomerate strength, Powder Metallurgy 31, 28-31.
Khakhar, D.V., Rising, H., and Ottino, J.M. (1986) An analysis of chaotic mixing in two chaotic flows, J. Fluid Mech., 172, 419-451.
Khakhar, D.V. and Ottino, J.M. (1986a) Fluid mixing (stretching) by time periodic sequences for weak flows, Phys. Fluids, 29, 11, 3503-3505.
Khakhar, D.V. and Ottino, J.M. (1986b) A note on the linear vector model of Olbricht, Rallison, and Leal as applied to the breakup of slender axisymmetric drops, J. Non-Newtonian Fluid Mech., 21, 127-131.
Khakhar, D.V. and Ottino, J.M. (1986c). Deformation and breakup of slender drops in linear flows, J. Fluid Mech., 166, 265-285.
Khakhar, D.V. and Ottino, J.M. (1987a) Breakup of liquid threads in linear flows, Int. J. Multiphase Flow, 13, 1, 71-86.
Khakhar, D.V., Franjione, J.G. and Ottino, J.M.(1987b) A case study of chaotic mixing in deterministic flows: the partitioned pipe mixer, Chem. Eng. Sci., 42, 2909-2926.
Kolmogorov, N. A. (1941) Uber das logarithmisch normale verteilungsgesetz der dimensionen der teilchen bei Zerstuckelung, Doklady Akad. Nauk. SSSR 31, 99-101. Translated in English by Levin in NASA-TT F-12,287 (1969).
Kuhn, W. (1953) Spontane Aufteilung von Flussigkeitszylindern in Klein Kugeln, Kolloid Z., 132, 84-99.
Kumar, S. and Homsy, G.M. (1996) Chaotic advection in creeping flow of viscoelastic fluids between slowly modulated eccentric cylinders, Phys. Fluids, 8, 1774-1787.
Kusch, H.A. and Ottino, J.M. (1992) Experiments on mixing in continuous chaotic flows, J. Fluid Mech., 236, 319-348.
Lee, Y. J., Feke, D. L. and Manas-Zloczower, I. (1993) Dispersion of titanium dioxide agglomerates in viscous media, Chem. Eng. Sci. 48, 3363-3372.
Leong, C.W. (1989) Experiments on mixing due to chaotic advection in a cavity, J. Fluid Mech., 209, 463-499.
Leong, C.W. (1990) Chaotic mixing of viscous fluids in time-periodic cavity flows, PhD thesis, Univ. Masachusetts, Amherst.
Levich, V.G. (1962) Physicochemical Hydrodynamics, Prentice-Hall, Englewood Cliffs, NJ, USA.
Liu, Y.H nd Zumbrunnen (1996) Emergence of fibrillar composites due to chaotic mxing of molten polymers, Polymer Composites, 17, 187-197.
Liu, Y.H nd Zumbrunnen (1997) Toughness enhancement in polymer blends due to th ein-situ formation of fine-scale extended strctures a low minor phase concentrations, J. Materials Sci., under review.
Manas-Zloczower, I. (1994) Dispersive mixing of solid additives in Mixing and Compounding of Polymers -- Theory and Practice, I. Manas-Zloczower and Z. Tadmor editors, Hanser Publishers, Munich, pp. 55-83.
Manas-Zloczower, I. and Feke, D. L. (1988) Analysis of agglomerate separation in linear flow fields, Intern. Polym. Process. II 3/4, 185-190.
Manas-Zloczower, I., Nir, A. and Tadmor, Z. (1982) Dispersive mixing in internal mixers-- a theoretical model based on agglomerate rupture, Rubber Chem. Tech. 55, 1250-1285.
Manas-Zloczower, I., Nir, A. and Tadmor, Z. (1984) Dispersive mixing in rubber and plastics, Rubber Chem. Tech., 57, 583-620.
Mason, T.G. and Bibette, J. (1996) Emulsification in viscoelastic media, Phys. Rev. Lett., 77, 3481-3484.
McGrady, E. D. and Ziff, R. M. (1987) Shattering transition in fragmentation, Phys. Rev. Lett. 58, 892-895.
McGrady, E. D. and Ziff, R. M. (1988) Analytical solutions to fragmentation equations with flow, AIChE J. 34, 2073-2076.
Meakin, P. (1988) Models for colloidal aggregation, Ann. Rev. Phys. Chem. 39, 237-269.
Meakin, P. (1992) Aggregation kinetics, Physica Scripta 46, 295-331.
Meijer, H.E.H., Lemstra, P.J., and Elemans, P.M.H. (1988) Structured polymer blends, Makromol. Chem., Makromol. Symp. 16, 113-135.
Meijer, H.E.H. and Janssen, J.M.H. (1994) Mixing of immiscible liquids, in Mixing and Compounding of Polymers -- Theory and Practice, I. Manas-Zloczower and Z. Tadmor editors, Hanser Publishers, Munich, pp. 85-147.
Mikami, T., Cox, R.G., and Mason, S.G. (1975) Breakup of extending liquid threads, Int. J. Multiphase Flow, 2, 113-138.
Morse, P. M. and Feshbach, H. (1953) Methods of Theoretical Physics, McGraw-Hill Book Company, Inc.: New York.
Muzzio, F. J. and Ottino, J. M. (1988) Coagulation in chaotic flows, Phys. Rev. A 38, 2516-2524.
Muzzio, F.J., Swanson, P.D., and Ottino, J.M. (1991) The statistics of stretching and stirring in chaotic flows, Phys. Fluids A, 5, 822-834.
Muzzio, F.J., Tjahjadi, M. and Ottino, J.M. (1991) Self-similar drop size distributions produced by breakup in chaotic flows, Phys. Rev. Lett., 67, 54-57.
Niederkorn, T.C., and Ottino, J.M. (1993) Mixing of viscoelastic fluids in time-periodic flows, J. Fluid Mech. 256, 243-268.
Niederkorn, T.C., and Ottino, J.M. (1994) Mixing of shear thinning fluids in time-periodic flows, AIChE Journal, 40, 1782-1793.
Neil, A. U. and Bridgwater, J. (1994) Attrition of particulate solids under shear, Powder Technol. 80, 207-209.
Olbricht, W.L., Rallison, J.M. and Leal, L.G. (1982) Strong flow criteria based on microstructure deformation, J. Non-Newtonian Fluid Mech., 10, 291-318.
Ottino, J.M. (1989) The Kinematics of Mixing: Stretching, Chaos, and Transport, Cambridge Univ. Press, Cambridge UK. 2nd printing, 1990.
Ottino, J. M. (1990) Mixing, chaotic advection and turbulence, Ann. Rev. Fluid Mech., 22, 207-253.
Patlazhan, S.A. and Lindt, J.T. (1996) Kinetics of structure development in liquid-liquid dispersions under simple shear flow. Theory, J. Rheol., 40, 1095-1113.
Parfitt, G. D. (1992) The mixing of cohesive powders. In Mixing in the Process Industries, N. Harnby, M. F. Edwards and A. W. Nienow (ed.) Elsevier Science Publishers B. V.: North-Holland, 321-348.
Powell, R. L. and Mason, S. G. (1982) Dispersion by laminar flow, AIChE J. 28, 286-293.
Rallison, J.M. (1981) A numerical study of the deformation and burst of a viscous drop in general shear flows, J. Fluid Mech., 109, 465-482.
Rallison, J.M. (1984) The deformation of small viscous drops and bubbles in shear flows, Ann. Revs. Fluid Mech., 16, 45-66.
Rauwendaal, C. (1994) Polymer Extrusion, 3rd ed., Hanser Publishers, Munich.
Redner, S. (1990) Fragmentation In Statistical Models for the Fracture of Disordered Media, H. J. Herrman and S. Roux (ed.) Elsevier Science Publishers B. V.: North-Holland, 321-348.
Robinson, D.J. and Earnshaw, J.C. (1992) Experimental study of aggregation in two dimensions. I. Structural aspects, Phys. Rev. A, 46, 2045-2054.
Rumpf, H. (1962) The strength of granules and agglomerates In Agglomeration, W. A. Knepper (ed.) John Wiley Interscience, New York.
Rumscheidt, F.D. and Mason, S.G. (1961) Particle motions in sheared suspensions. XII. Deformation and burst of fluid drops in shear and hyperbolic flow, J. Colloid Sci., 16, 238-261.
Rwei, S. P., Manas-Zloczower, I. and Feke, D. L. (1990) Observation of carbon black agglomerate dispersion in simple shear flows, Polym. Eng. Sci. 30, 701-706.
Rwei, S. P., Manas-Zloczower, I. and Feke, D. L. (1991) Characterization of agglomerate dispersion by erosion in simple shear flows, Polym. Eng. Sci. 31, 558-562.
Rwei, S. P., Manas-Zloczower, I. and Feke, D. L. (1992) Analysis of the dispersion of carbon black in polymeric melts and its effect on compound properties, Polym. Eng. Sci. 32, 130-135.
Schepens, F.A.O. (1996) Chaotic mixing in the extended periodic cavity flow, Masters thesis, Eindhoven University of Technology.
Schowalter, W. R. (1984) Stability and coagulation of colloids in shear fields, Ann. Rev. Fluid Mech. 16, 245-261.
Schuman, T.E.W. (1940) Theoretical aspects of the size distribution of fog particles, Quart. J. Meteorological. Soc., 66, 195-208.
Smoluchowski, M. (1917) Versuch einer mathematischen theorie der koagulatinskinetik kolloider lösungen, Z. Phys. Chem. 92, 129-168.
Sonntag, R. C. and Russel, W. B. (1986) Structure and breakup of flocs subject to fluid stresses. I Shear experiments, J. Colloid Interface Sci. 113, 399-413.
Sonntag, R. C. and Russel, W. B. (1987a) Structure and breakup of flocs subject to fluid stresses. II Theory, J. Colloid Interface Sci. 115, 378-389.
Sonntag, R. C. and Russel, W. B. (1987b) Structure and breakup of flocs subject to fluid stresses. III Converging flow, J. Colloid Interface Sci. 115, 390-395.
Spielman, L. A. (1970) Viscous interactions in Brownian coagulation, J. Colloid Interface Sci. 33, 562-571.
Srinivasan, M.P. and Stroeve, P. (1986) Subdrop ejection from double emulsion drops in shear flow, J. Membrane Sci. 26, 231-236.
Stone, H. A. (1994) Dynamics of drop deformation and breakup in viscous fluids, Ann. Revs. Fluid Mech. 26, 65-102.
Stone, H.A. and Leal, L.G. (1989) Relaxation and breakup of an initially extended drop in an otherwise quiescent fluid, J. Fluid Mech., 198, 399-427.
Stone, H.A., Bentley, B.J., and Leal, L.G. (1986) An experimental study of transient effects in the breakup of viscous drops, J. Fluid Mech., 173, 131-158.
Stroeve, P. and Varanasi, P.P. (1984) An experimental study of double emulsion drop breakup in uniform shear flow, J. Coll. Int. Sci, 99, 360-373.
Sundaraj, U., Dori, Y. and Macosko, C.W. (1995) Sheet formation in immiscible polymer blends: model experiments on an initial blend morphology, Polymer, 36, 1957-1968.
Tanner, R.I. (1976) A test particle approach to flow classification for viscoelastic fluids, AIChE J., 22, 910-918.
Taylor, G.I. (1932) The viscosity of a fluid containing a small drops of another fluid, Proc. R. Soc., A138, 41-48.
Tjahjadi, M. and Ottino, J.M. (1991) Stretching and breakup of droplets in chaotic flows, J. Fluid Mech., 232, 191-219.
Tjahjadi, M., Stone, H.A., and Ottino, J.M. (1992) Satellite and subsatellite formation in capillary breakup, J. Fluid Mech., 243, 297-317.
Tomotika, S. (1935) On the instability of a cylindrical thread of a viscous liquid surrounded by another viscous fluid, Proc. R. Soc., A150, 322-337.
Tomotika, S. (1936) Breaking up of a drop of viscous liquid immersed in another viscous fluid which is extending at a uniform rate, Proc. R. Soc., A153, 302-318.
Torres, F. E., Russel, W. B. and Schowalter, W. R. (1991a) Floc structure and growth kinetics for rapid shear coagulation of polystyrene colloids, J. Colloid Interface Sci. 142, 554-574.
Torres, F. E., Russel, W. B. and Schowalter, W. R. (1991b) Simulations of coagulation in viscous flows, J. Colloid Interface Sci. 145, 51-73.
Ulbrecht, J.J., Stroeve, P. and Pradobh, P. (1982) Behavior of double emulsions in shear flows, Rheol. Acta, 21, 593-597.
Varanasi, P.P, Ryan, M.E., and Stroeve, P. (1994) Experimental study on the breakup of model viscoelastic drops in uniform shear flow, I&EC Reserach 33, 1858-1866.
van Dongen, P. G. J. and Ernst, M. H. (1988) Scaling solutions of Smoluchowski's coagulation equation, J. Stat. Phys. 50, 295-329.
Verwey, E.J. and Overbeek, J.T.G. (1948) Theory of the Stability of Lyophobic Colloids, Elsevier.
Villadsen, J. (1997) Putting structure into chemical engineering, Chem. Eng. Sci., 52, 2857-2864
Wang, H., Zinchenko, A. and Davis, R.H. (1994) The collision rate of small drops in linear flow fields, J. Fluid Mech., 265, 161-188.
White, J.L. (1990) Twin Screw Extrusion, Hanser Publisher, Munich.
Williams, M. M. R. (1990) An exact solution of the fragmentation equation, Aerosol Sci. and Tech. 12, 538-546.
Zeichner, G.R. and Schowalter, W.R. (1977) Use of trajectory analysis to study stability of colloidal dispersions in flow fields, AIChE J., 23, 243-254.
Zhang, D.F. and Zumbrunnen, D.A. (1996a) Chaotic mixing of two similar fluids in the presence of a third dissimilar fluid, AIChE J., 42, 3301-3309.
Zhang, D.F. and Zumbrunnen, D.A. (1996b) Influences of fluidic interfaces on the formation of fine scale strctures by chaotic mixing, J. Fluids Eng., 118, 40-47.
Ziff, R. M. (1991) New solutions to the fragmentation equation, J. Phys. A: Math. Gen. 24, 2821-2828.
Ziff, R. M. and McGrady, E. D. (1985) The kinetics of cluster fragmentation and depolymerisation, J. Phys. A: Math. Gen. 18, 3027-3037.
Ziff, R. M. and McGrady, E. D. (1986) Kinetics of polymer degradation, Macromolecules 19, 2513-2519.
Zumbrunnen, D.A., Miles, K.C., and Liu, Y.H. (1996) Auo-processing of very fine-scale materials by chaotic mixing of melts, Composites, 27A, 37-47.
Figure 2: Mixing in the vortex mixing flow with increasing periods of flow (P). The flow is time periodic with each cylinder rotating alternately for a fixed time period. (Jana, Metcalfe and Ottino, 1994)
Figure 3: Mixing in the cavity flow. The flow is time periodic with the upper and lower walls moving alternately for a fixed time period. (Leong and Ottino, 1989)
Figure 4: Mixing in the time periodic cavity flow at increasing values of the time period. The mixed state is shown at long mixing times. (Leong and Ottino, 1989)
Figure 5: Mixing in the partitioned pipe mixer. (a) Schematic view of the mixer geometry; one element of the mixer is shown, and the mixer comprises several such elements joined together. (b) KAM surfaces in flow bounding regions of regular flow. (c) Experimentally obtained streaklines: undeformed streaklines pass through KAM tubes whereas streaklines in the chaotic region are well mixed. (Khakhar, Franjione and Ottino, 1987; Kusch and Ottino, 1992)
Figure 6: (a) Schematic view of an extruder channel with an undulating baffle. (b) B,C,D: Steady flow streamlines with and without baffles for initial condition A. E,F: Mixing in a cavity flow with an oscillating baffle. The upper plate moves with a steady velocity while the lower plate with the baffle undergoes linear oscillatory motion. (Jana, Tjahjadi and Ottino, 1994)
Figure 7: Experiments and computations on the advection of a dye blob in an
eccentric cylinder apparatus (from Niederkorn and Ottino (1993)). Left: Top -
experiment using Newtonian fluid; Bottom - numerical simulation of same
situation. Right: Top - identical experiment as in upper left, but using
viscoelastic fluid (We ![]() 0.06); Bottom - numerical
simulation using We = 0.04.
0.06); Bottom - numerical
simulation using We = 0.04.
Figure 8: (a) Distribution of length stretches (logl) for increasing periods of flow (n) in a journal bearing flow. The distribution approaches a log normal form (parabolic shape) at large n. (b) Rescaled distribution of length stretches. Data in (a) collapse to a single curve implying self-similarity. (Muzzio et al., 1991)
Figure 9: Average efficiency of stretching
of material elements ![]() in a simple shear flow with random reorientation after an average
length stretch gm. r gives the with of the
distribution of length stretch about the mean value (gm).
Results for a random distribution (top) and a normal distribution (bottom) of
length stretch are shown. The maximum in the efficiency corresponds to the
maximum length stretch for a fixed amount of energy dissipated and occurs at an
average stretch of about 5 per period. (Khakhar and Ottino, 1986a)
in a simple shear flow with random reorientation after an average
length stretch gm. r gives the with of the
distribution of length stretch about the mean value (gm).
Results for a random distribution (top) and a normal distribution (bottom) of
length stretch are shown. The maximum in the efficiency corresponds to the
maximum length stretch for a fixed amount of energy dissipated and occurs at an
average stretch of about 5 per period. (Khakhar and Ottino, 1986a)
Figure 10: Scanning electron micrograph of
a fracture surface parallel to the direction of extrusion of an extrudate of a
45:55 PS-HDPE blend with a viscosity ratio ![]() . Fibrous PS is shown at different
stages of breakup; the diameter of the largest fiber is about 1 mm (Meijer et al.,
1988).
. Fibrous PS is shown at different
stages of breakup; the diameter of the largest fiber is about 1 mm (Meijer et al.,
1988).
Figure 11: Schematic view of the stages in the mixing of two immiscible viscous liquids. The large drop of the dispersed phase is stretched out and folded by the flow, and breaks up into smaller droplets. Smaller drops may collide and coalesce to form larger drops.
Figure 12: Deformation of the interface between two immiscible viscous liquids in a steady cavity flow with increasing time of flow. The viscosity ratio is p=0.8, and the upper fluid is of lower viscosity. (Chakravarthy and Ottino, 1996).
Figure 13: Streamlines and velocity profiles for two dimensional linear flows with varying vorticity. (a) K=-1: pure rotation, (b) K=0: simple shear flow, (c) K=1: hyperbolic extensional flow.
Figure 14: Critical capillary number (Cacrit) as a function of the viscosity ratio (p) for two dimensional linear flows with varying vorticity. (Bentley and Leal, 1986)
Figure 15: Affine stretching of a filament in the journal bearing flow. Experiments (top) agree well with computations (bottom) carried out assuming that the filament deforms as the suspending fluid (i.e., affine deformation). (Tjahjadi and Ottino, 1991)
Figure 16: Drop breakup in the journal bearing flow. The drop initially in the chaotic region of the flow deforms into a thin filament which breaks to produce a fine dispersion of droplets. The drop initially in the regular region of the flow (island) remains undeformed. (Tjahjadi and Ottino, 1991)
Figure 17: Stretching of a filament in a
simple shear flow with random reorientation at different time intervals. The
length stretch is shown versus time for ![]() .
.
Figure 18: Graphical interpretation of the criterion for breakup of pointed drops in an extensional flow. (Khakhar and Ottino, 1986b)
Figure 19: Schematic view of the different mechanisms of drop breakup. The mechanism operative in a particular case is determined by p, Ca and the flow type.
Figure 20: Radius of drops produced on
capillary breakup in hyperbolic extensional flow (Rdrops),
radius of the thread at which the disturbance that causes breakup begins to grow
(Rcrit), and the time for growth of
the disturbance (tgrow) for different values of the
dimensionless parameters p and ![]() . The time for capillary breakup of
the extending thread (tbreak) can be obtained from these
graphs (see Illustration for sample calculations). (Janssen and Meijer,
1993)
. The time for capillary breakup of
the extending thread (tbreak) can be obtained from these
graphs (see Illustration for sample calculations). (Janssen and Meijer,
1993)
Figure 21: Formation of satellite drops during the breakup of a filament at rest. A comparison between computations and experimental results is shown. (Tjahjadi, Stone and Ottino, 1992)
Figure 22: Radius of drops produced by
capillary breakup (solid lines) and binary breakup (dotted lines) in a
hyperbolic extensional flow for different viscosity ratios (p) and scaled shear
rate (![]() ) (Janssen and
Meijer, 1993). The initial amplitude of the surface disturbances is a0=10-9 m. Note that significantly smaller
drops are produced by capillary breakup for high viscosity ratios.
) (Janssen and
Meijer, 1993). The initial amplitude of the surface disturbances is a0=10-9 m. Note that significantly smaller
drops are produced by capillary breakup for high viscosity ratios.
Figure 23: Distribution of drop sizes for mother droplets and satellite droplets (solid lines) produced during the breakup of a filament in a chaotic flow. The total distribution is also shown (dashed line).
Figure 24: Experimental results for drop breakup in a journal bearing flow. The figure on the right shows repeated stretching and breakup, which is observed for low viscosity drops (Tjahjadi and Ottino, 1991).
Figure 25: Drop size distributions (f(V,p)) based on drop volume (V) obtained by repeated stretching and breakup in a journal bearing flow for different viscosity ratios (p) (left). The curves for the different distributions overlap when the distribution is rescaled (right) (Muzzio, Tjahjadi and Ottino, 1991).
Figure 26: Schematic representation of the three basic steps of coalescence.
Figure 27: Various modes of film drainage and the corresponding equations for the rate of film thinning and drainage time are shown. The criteria for specific modes are also indicated.
Figure 28: Size distributions from a
typical simulation produced by the VILM model. After six cycles a steady size is
reached. Smaller sizes are obtained after five cycles as compared to the final
distribution. The conditions for the simulation are: ![]()
Figure 29: Average steady-state size of the dispersed phase at different viscosity ratios. The solid and dashed lines represent simulations in which md and mc are held constant. Other process parameters are the same as used for Figure 28 (except f=0.05). It is clear that the magnitudes of both viscosities must be considered rather than just the viscosity ratio. The lowest viscosity in each case is 1 Pa s and the highest 1000 Pa s. The curves are equally spaced on a logarithmic scale for viscosity.
Figure 30: Schematic view of rupture and erosion of particles and the typical size distribution of fragments obtained.
Figure 31: Fractal structures obtained experimentally at different stages of aggregation of a colloidal monolayer of 1 mm sulphonated polystyrene particles on the surface of an aqueous calcium chloride solution, initially uniformly distributed (Robinson and Earnshaw, 1992).
Figure 32: Relationship between Facrit and the dimensionless cluster size (R/a) for fractal clusters (D?2.5) of polystyrene latex in a simple shear flow. Data points are experimental results and the solid line is the theoretical prediction. (Sonntag and Russel, 1986,1987a)
Figure 33: Variation of dimensionless radius with dimensionless time for compact carbon black particles suspended in silicone oil undergoing a simple shear flow. Top: data for initial radius R0?1.7 mm for different viscosities and different shear rates but with Fa?0.28. Bottom: data for initial radius R0?2.0 mm for different densities and different shear rates but with Fa?0.28. For all cases the erosion rate constant ke?0.37.
Figure 34: Top: Schematic view of a Banbury mixer. Bottom: Evolution of the agglomerate size distribution with time predicted by the two zone model with parameter values corresponding to the dispersion of carbon black in rubber in a Banbury mixer. The size of an agglomerate after j ruptures is given by Dj=D0/2j/3 where D0 is the initial size of the agglomerates. The size of the aggregate (primary particle) corresponds to j=28. (Manas-Zloczower, Nir and Tadmor, 1982)
Figure 35: (a) Size distributions (c(x,q)) obtained for erosion controlled fragmentation for increasing fragmentation time (q). (b) Comparison of theoretically predicted cumulative size distribution for erosion controlled fragmentation to experimental data. (Hansen and Ottino, 1996a)
Figure 36: The spatial variation of agglomerate sizes in simulations of erosion in the journal bearing flow. Initially there are 10000 agglomerates consisting of 400-500 aggregates. Colors: red- less than 200 aggregates, yellow- 200 to 300 aggregates, green- 300 to 400 aggregates, blue- more than 400 aggregates. (a) Poorly mixed flow after four periods. (b) Well mixed flow after one period. (Hansen, 1997)
Figure 37: Typical clusters obtained by diffusion limited aggregation (DLA). Top: Two dimensional diffusion limited aggregation. Bottom: Reaction limited hierarchical cluster-cluster aggregation (HCCA). (Meakin, 1988)
Figure 38: Variation of polydispersity with average cluster size at short times in a journal bearing flow. The symbols are from simulations and the lines are fits from Eq. (B.44). The regular flow is the journal bearing flow with only the inner cylinder rotating. (Hansen and Ottino, 1996b)
Figure 39: (a) The growth of average cluster size for clusters with a constant capture radius in various 2D flows. (b) Variation of polydispersity with average cluster size. (c) Scaled distribution of the cluster sizes at different times. The regular flow is the journal bearing flow with only the inner cylinder rotating. One time unit is equivalent to the total displacement of the boundaries equal to the circumference of the outer cylinder. (Hansen and Ottino, 1996b)
Figure 40: Growth of average cluster size for area conserving clusters and fractal clusters in the journal bearing flow. (Hansen and Ottino, 1996b)
Figure 41: Typical 2D fractal structure obtained by aggregation of particles in the journal bearing flow. Fractal dimension of the cluster is 1.54. (Hansen and Ottino, 1996b)
Figure 42 Distribution of the fractal dimensions of the clusters generated by aggregation in the journal bearing flow for different flow types. (Hansen and Ottino, 1996b)
Figure 43 Capillary breakup of closely spaced molten nylon-6 threads in molten polystyrene. Photograhs at different times are shown (frames "a" through "f" correspond to 0, 210, 270, 360,390 and 510 s). The initial thread diameter is 70 mm (Elemans et al., 1997).